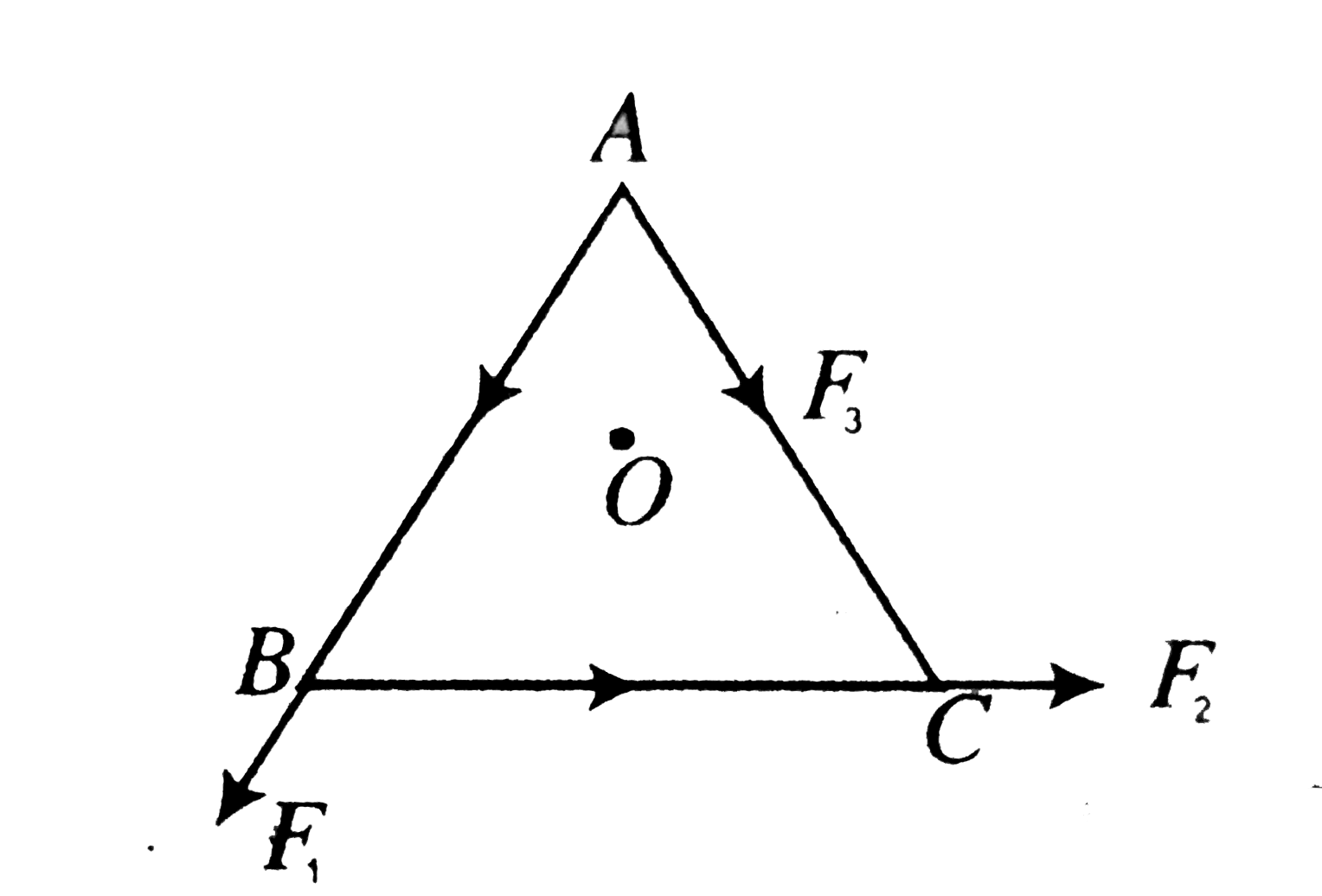
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
2(F1+F2)
F1+F22
F1−F2
F1+F2
The correct Answer is:D
The torquues F1d and F2d of F1 and F2 respectively are counterclockwise. The torque F3d is clockwise. Applying condition for rotational equilibrium

F1d+F2d−F3d=0 or F3=F1+F2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Multiple Correct
Explore 9 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Linked Comprehension
Explore 28 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Subjective
Explore 13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
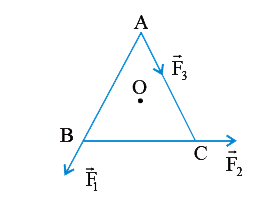
ABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
View SolutionABC is a triangle in which D, E and F are the mid-points of the sides AC, BC and AB respectively. What is the ratio of the area of the shaded to the unshaded region in the triangle?

View Solution
Knowledge Check
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of F3, so that the total torque about O is
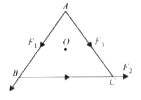 A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)
A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCparallelogramDrhombusIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
In the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
View SolutionGiven an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
View Solution

