A thin homogeneous lamina is in the form of a circular disc of radius R. From it a circular hole exactly hall the radius of the lamina and touching the lamina's circumference is cut off. Find the centre of mass of the remaining part.

Video Solution

Text Solution

Verified by Experts

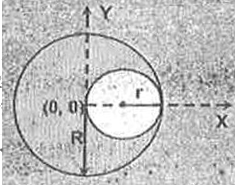
Let the centre of the lamina be the origin. Due to symmetry, the C.M. will lie on the x - axis. Let m be the mass of the circular lamina. Then, mass m. of the removed circular hole is
$m . = \frac{M}{π R^{2}} (π r^{2}) = \frac{M}{R^{2}} {(\frac{R}{2})}^{2} = \frac{M}{4}$
$∴ x_{c m} = \frac{M .0 - m . . r}{M - m .}$
The negative sign of m. denotes that it has been removed.
$x_{c m} = \frac{- \frac{M}{4} \frac{R}{2}}{M - \frac{M}{4}} = - \frac{R}{6}$
Thus, the centre of mass of the remaining part lies at a distance R/6 towards left of the origin, i.e., the initial centre of mass of the disc.

Updated on:21/07/2023

A uniform metal dise of radius R is taken and out of it a disc of diameter R is cut off from the end. The centre of the mass of the remaining part will be:
A $\frac{R}{4}$ from the centre
B $\frac{R}{3}$ from the centre
C $\frac{R}{5}$ from the centre
D $\frac{R}{6}$ from the centre
A uniform metal disc of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
A $\frac{R}{4}$ from the center
B $\frac{R}{3}$ from the center
C $\frac{R}{5}$ from the center
D $\frac{R}{6}$ from the center.
A solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 Cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy. (Use $π = 22 / 7$ and $\sqrt{149} = 12.2$ )
A $\frac{R}{3}$
B $\frac{R}{2}$
C $\frac{R}{6}$
D $\frac{R}{4}$