From a uniform circular disc of diameter D, a circular disc or hole of diameter D/6 and having its centre at a distance of D/4 from the centre of the disc is scopped out. Determine the centre of mass of the remaining portion.
Step by step video & image solution for From a uniform circular disc of diameter D, a circular disc or hole of diameter D//6 and having its centre at a distance of D//4 from the centre of the disc is scopped out. Determine the centre of mass of the remaining portion. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem for self practice
Explore 90 Videos
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem for self practice
Explore 90 Videos
- PROPERTIES OF SOLIDSBook:SL ARORAChapter:PROPERTIES OF SOLIDSExercise:All Questions
Explore 97 Videos
- System of particles & rotational MotionBook:SL ARORAChapter:System of particles & rotational MotionExercise:EXERCISE
Explore 353 Videos
Similar Questions
From a uniform circular disc of diameter d,a circular disc of diameter d/6 and having centre at a distance d/4 from the centre of the disc is scooped out. Determine the centre of mass of remaining portion.
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View Solution
Knowledge Check
A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)From a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)
A4R3(π−2)B2R3(π−2)C5R7(π−2)DR3(π−1)A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2a2−c2Bcb2a2−b2Cπc2a2−b2Dca2(c2−b2)
Aπb2a2−c2Bcb2a2−b2Cπc2a2−b2Dca2(c2−b2)
Find the centre of mass of the shaded portion of a disc.
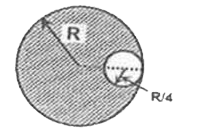
View SolutionFind the centre of mass of the shaded portion of a disc
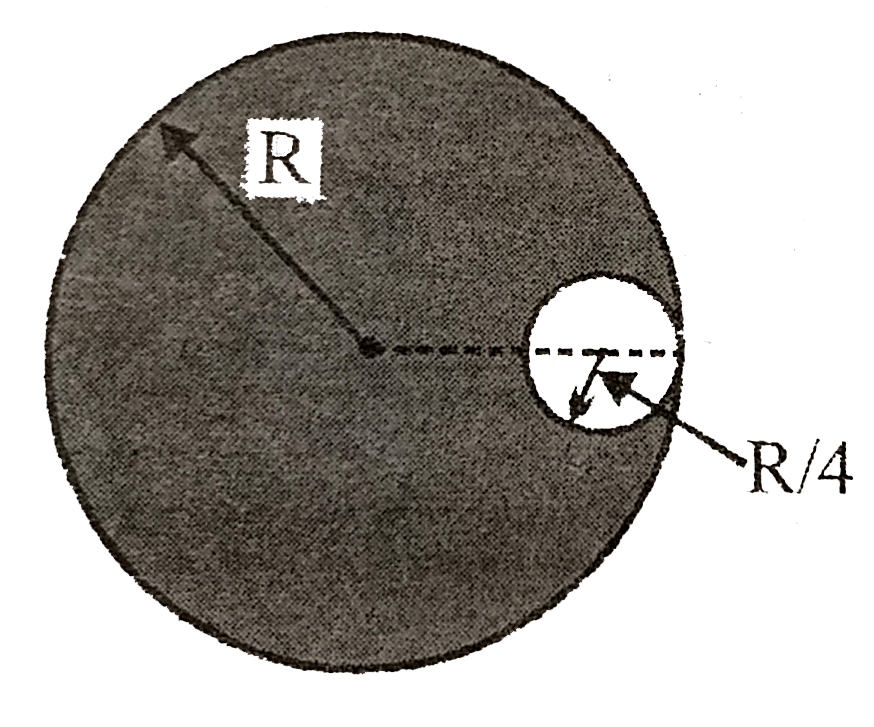
View SolutionA circular disc of radius R4 is cut from a uniform circular disc of radius R.
The centre of cut portion is at a distance of R2 from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View Solution

