Determine the centre of mass of a uniform hemisphere of radius R.

Video Solution

Text Solution

Verified by Experts

$X_{c m} = 0$ (by symmetry)
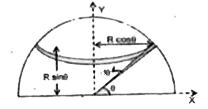
$Y_{c m}$ can be calculated by considering a small element (taken by drawing two circles on its surface at angles $θ$ and $θ + d θ$ as shown).
Surface mass density $= σ = \frac{M}{2 π R^{2}} = \frac{d m}{d A}$
$d m = \frac{M}{2 π R^{2}} 2 π R cos θ R d θ = M cos θ d θ$
$Y_{c m} = \frac{1}{M} \int d m = \frac{1}{M} \int y M cos θ d θ = \int_{0}^{π / 2} R sin θ cos θ d θ (∵ y = R sin θ)$
On solving, we get
$Y_{C M} = R / 2$
$∴$ C.M. of thin uniform hemispherical shell is $(0, \frac{R}{2})$

Updated on:21/07/2023

|

Class 12 PHYSICS COLLISION

Topper's Solved these Questions

Similar Questions

Knowledge Check

The distance of the centre of mass of a hemispherical shell of radius R from its centre is
A $\frac{R}{2}$
B $\frac{R}{3}$
C $\frac{2 R}{2}$
D $\frac{2 R}{3}$

FIITJEE-COLLISION -Exercise

Home
Ask Doubt
Profile