A bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
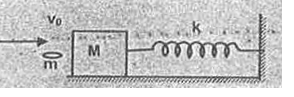
The process of impact of bullet and block is transient. Within a very short time of impact, the compression of the spring is negligible. Therefore, the corresponding spring force is negligible. Even though it is external to the system (M+m), we can conserve its momentum just before and after the impact (impact force is internal). Conservation of linear momentum of bullet plus block just before and after the impact (impact force is internal). Conservation of linear momentum of bullet plus block just after and before impact yields
(M+m)v=mv0
⇒v=mv0M+m
where v = common velocity of block and bullet.
Therefore the loss of K.E. of the system
ΔKE=12mv20−12(M+m)v2
Putting v=mv0M+m are obtain.
ΔKE=Mnv202(M+m).
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)
Explore 2 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Fill in the blanks)
Explore 3 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE) MATRIX MATCH TYPE
Explore 2 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
A bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

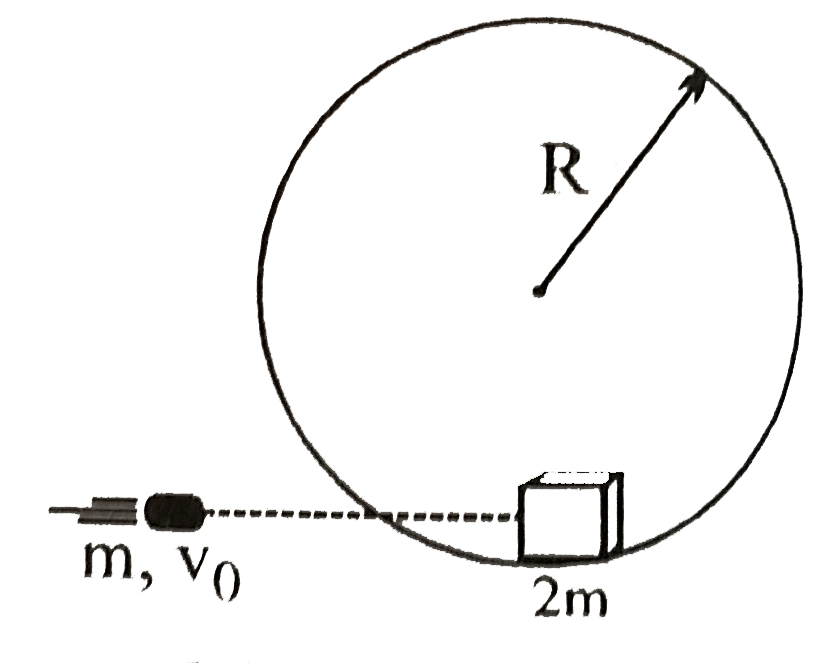
View SolutionA small block of mass 2m initially rests at the bottom of a fixed circular, vertical track, which has a radius of R. The contact surface between the mass and the loop is frictionless. A bullet of mass m strikes the block horizontally with initial speed v0 and remain embedded in the block as the block and the bullect circle the loop. Determine each of the following in terms of m,R and g.
(a) The speed of the masses immediately after the impact.
(b) The minimum initial speed of the bullet if the block and the bullet are to successfully execute a complete ride on the loop
View Solution
Knowledge Check
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
AMm+M(√2gRBM+mm√2gRC(Mm)√2gRDNone of theseA bullet of mass m is fired from a gun of mass M. The recoiling gun compresses a spring of force constant k by a distance d. Then the velocity of the bullet is
Akd√M/mBdM√kmCdm√kMDkMm√d
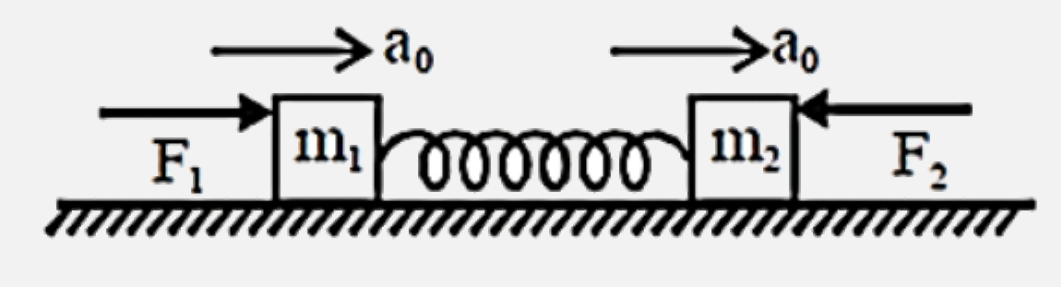
Two blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
View SolutionIn the figure shown, initially the spring is in relaxed position. A bullet of mass m hits the block 'A' with horizontal speed v0 and gets embedded into it. Find the maximum compression in the spring. Stiffness of the spring is K. Neglect any friction and deformation in the spring during collision.
View SolutionA bullted of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial sped of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time forthe bullet - block system to come to rest.
View SolutionTwo identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionA bullet of mass m strikes an obstruction and deviates off at 60° to its original direction. If its speed is also changed from u to v, find the magnitude of the impulse acting on the bullet.
View Solution

