Two blocks of masses and are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. bullet of mass moving with a velocity hits the hanging block of mass and gets exbedded in it. Find the height through which block rises after the collision.
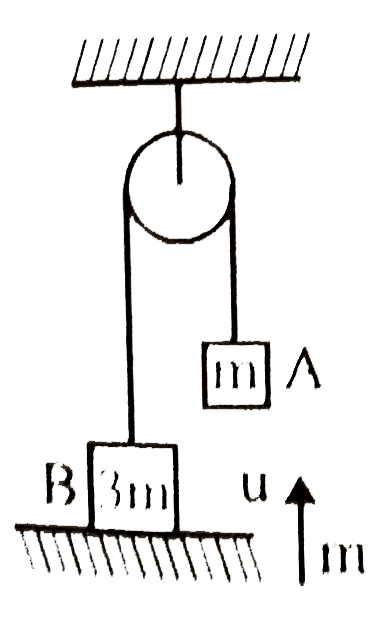
As soon as the collision occurs, the string becomes slack, tension becomes zero. Gravitational force is acting vertically downwards. But as gravitational force is a weaker force than impulse force, therefore a possible change of momentum due to gravitational force during collision can be neglected.
Hence, conserving momentum of the system during collision along vertical direction:
If v = velocity of the combined mass just after collision
Then,
Block A + bullet start moving with velocity u/2.
Now, maximum height through which the combined mass rises
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)
Explore 2 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Fill in the blanks)
Explore 3 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE) MATRIX MATCH TYPE
Explore 2 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
Two blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionFind the acceleration of masses m1 and m2 connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
View Solution
Knowledge Check
A bullet of mass m moving vertically upwards instantaneously with a velocity 'u' hits the hanging block of mass 'm' and gets embedded in it, as shown in the figure. The height through which the block rises after the collision. (assume sufficient space above block) is:
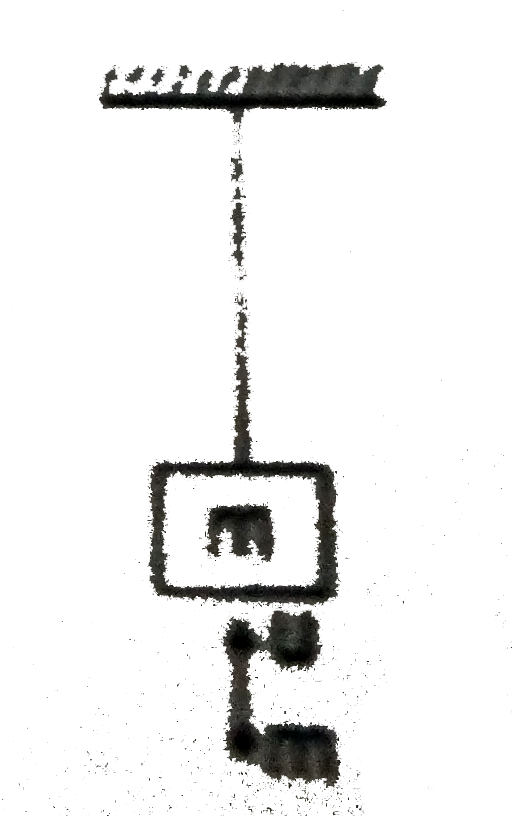 Au2/2gBu2/2gCu2/8gDu2/4g
Au2/2gBu2/2gCu2/8gDu2/4gTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionA system of two blocks A and B are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass m moving with a velocity u as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is

View SolutionTwo masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
View SolutionTwo blocks of mass m1andm2 are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
View Solution

