Find the acceleration of masses m1 and m2 connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
To find the acceleration of the masses m1 and m2 connected by an inextensible string over a massless and frictionless pulley, we can follow these steps:
Step 1: Identify the Forces Acting on Each Mass
- For mass m1 (on an inclined plane):
- The gravitational force acting downwards: m1g
- The component of gravitational force acting along the incline: m1gsinα
- The tension in the string acting upwards: T
- For mass m2 (hanging vertically):
- The gravitational force acting downwards: m2g
- The tension in the string acting upwards: T
Step 2: Write the Equations of Motion
Using Newton's second law, we can write the equations for each mass.
- For mass m1:
T−m1gsinα=−m1a(1)
(The negative sign indicates that m1 is accelerating down the incline.)
- For mass m2:
m2g−T=m2a(2)
(Here, m2 is accelerating downwards.)
Step 3: Solve the Equations Simultaneously
We can add equations (1) and (2) to eliminate T:
(T−m1gsinα)+(m2g−T)=−m1a+m2a
This simplifies to:
m2g−m1gsinα=(m2−m1)a
Step 4: Isolate the Acceleration a
Rearranging the equation gives:
a=m2g−m1gsinαm2+m1
Step 5: Final Expression for Acceleration
Thus, the acceleration a of the system is:
a=g(m2−m1sinα)m1+m2
- For mass m1 (on an inclined plane):
- The gravitational force acting downwards: m1g
- The component of gravitational force acting along the incline: m1gsinα
- The tension in the string acting upwards: T
- The gravitational force acting downwards: m2g
- The tension in the string acting upwards: T
Using Newton's second law, we can write the equations for each mass.
T−m1gsinα=−m1a(1)
(The negative sign indicates that m1 is accelerating down the incline.)
m2g−T=m2a(2)
(Here, m2 is accelerating downwards.)
We can add equations (1) and (2) to eliminate T:
(T−m1gsinα)+(m2g−T)=−m1a+m2a
This simplifies to:
m2g−m1gsinα=(m2−m1)a
Rearranging the equation gives:
a=m2g−m1gsinαm2+m1
Thus, the acceleration a of the system is:
a=g(m2−m1sinα)m1+m2
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Practice Exerice 2.1
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Practice Exerice
Explore 4 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
Find the acceleration of masses m1 and m2 moving down the smooth incline plane. The string and the pulley are masseless and frictionless.
View SolutionA situation is shown in figure-2.15, Find the acceleration of masses m1 abd m2 mass of pulley is mP. Consider the string going over the pulley is massless and frictionless.

View Solution
Knowledge Check
The acceleration of the block (A) and (B) respectively in situation shown in the figure is: (pulleys and string are massless).
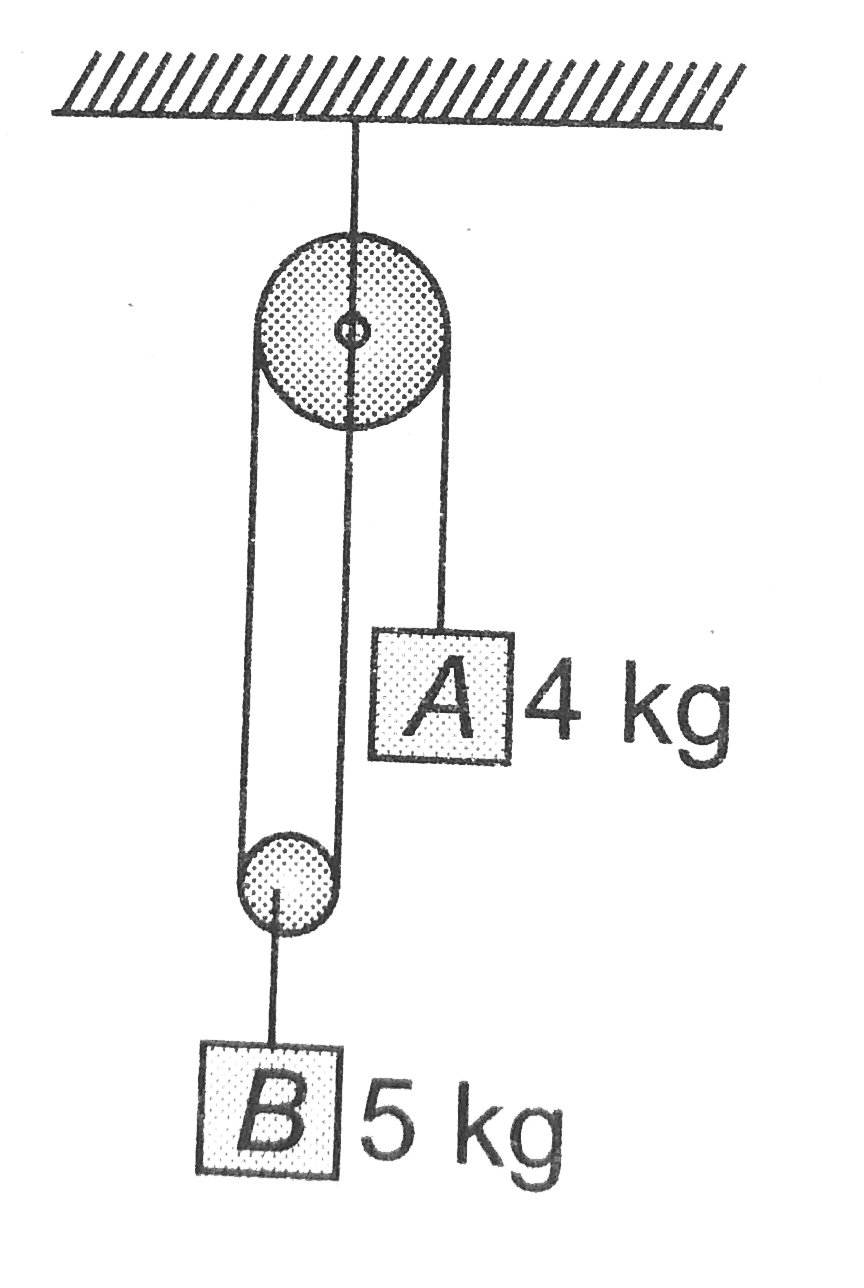 A2g7 downward, g7 upwardB2g3 downward, g3 upwardC1013g downward, 5g13 upwardDnone of these
A2g7 downward, g7 upwardB2g3 downward, g3 upwardC1013g downward, 5g13 upwardDnone of theseA system of two blocks A and B are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass m moving with a velocity u as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is
 A5mu4B4mu5C2mu5D3mu5
A5mu4B4mu5C2mu5D3mu5A lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
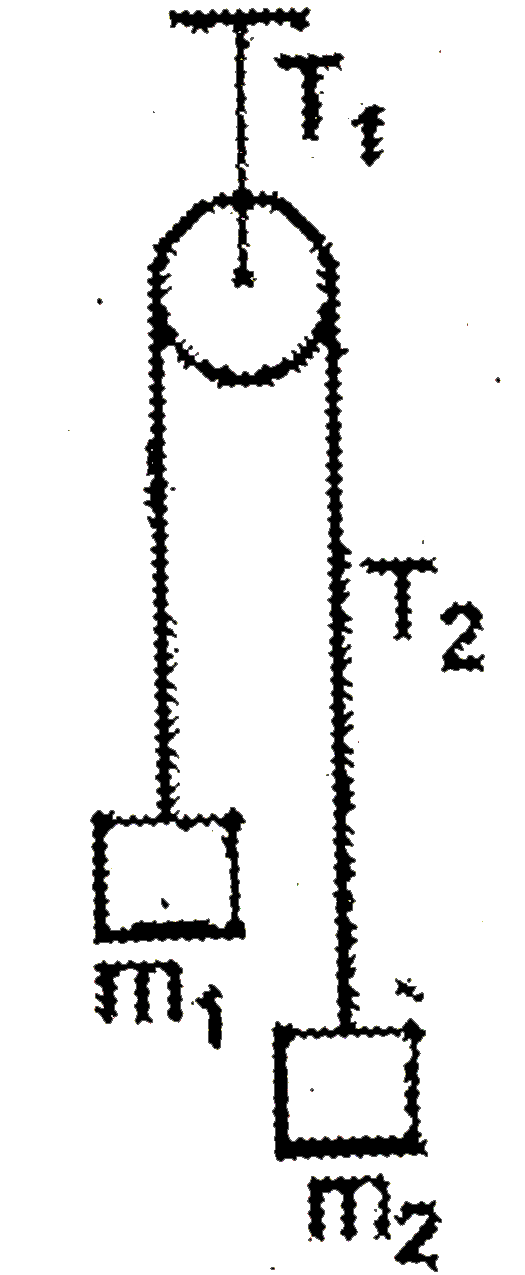
If m1+m2=m and lift is moving with constant velocity then value of T1 :A≥mgB=mgC≤mgD>mg
Two blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
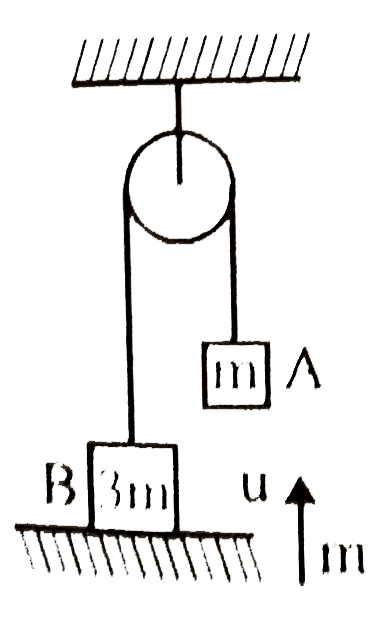
View SolutionIn the arrangement shown, find the acceleration of each block, tension in the string and reaction in the pulley. The string and pulley are light (massless) (m1>m2). Neglect the friction in pulley.

View SolutionTwo masses m1 and m2 are connected by a massless string as shown in Fig. Find the value of tension in the string if a force of 200 N is applied on (i) m1 and m2.

View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer

If m1 is very small as compared to m2 and lift is moving with constant velocity then value of T2 is nearly :
View SolutionTwo masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is

View Solution

