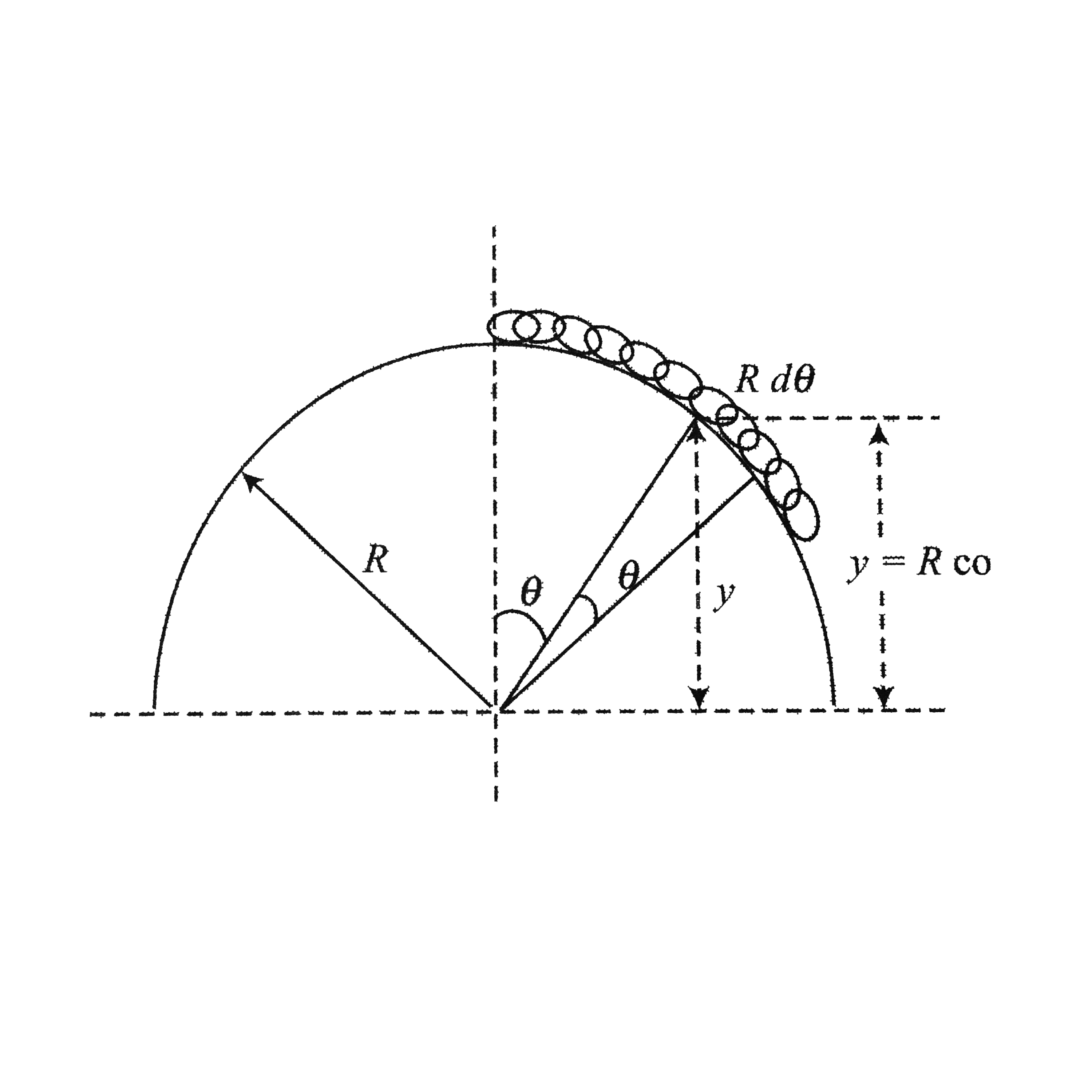
A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain .
The correct Answer is:
Step by step video, text & image solution for A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain llt1/2piR. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Advance MCQs
Explore 17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
Similar Questions
A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View SolutionA uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.
View Solution
Knowledge Check
A chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle θ=π4.A23.4JB63.44JC80 JD97.4JA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The tangential acceleration of the chain when its starts sliding down.A40π(1−1√2)B20π(1−1√2)C10(1−1√2)DzeroA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The gravitational potential energy of the chain considering reference level at the base of hemisphere isA20 JB20√2JC40 JD40√2J
AS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.
View SolutionA chain AB of length l is located in a smooth horizontal tube so that its fraction of length h hangs freely and touches the surface of the table with its end B(figure). At a certain moment the end A of the chain is set free. With what velocity will this end of the chain slip out of the tube?

View SolutionA chain of length L and mass m is placed upon a smooth surface. The length of BA is (L−b). Calculate the velocity of the chain when its and reaches B

View SolutionA uniform chain of length l and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
View Solution

