A chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.
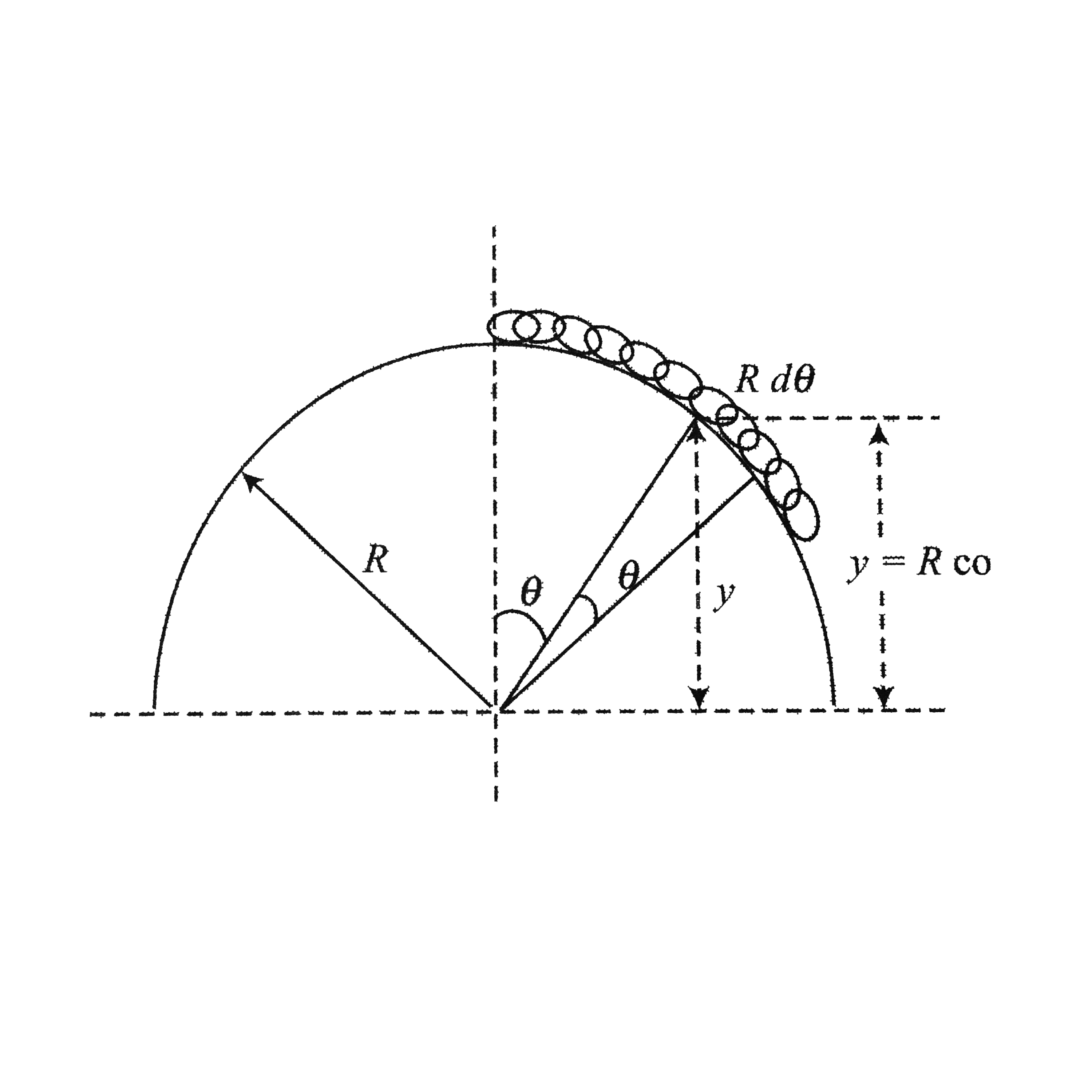
The mass is distributed in chain uniformly along its length.
Choose a small element of chain of width dthη at an angle θ from the vertical.
The mass of the element, dm=(mlRdθ)
The gravitational potential energy of the element dU=(dm)gy
Thus, the gravitational potential energy of whole chain
U=∫(dm)gy
=(l/R)∫0(mlRdθ)g(Rcosθ)
=mR2gl(lR)∫0cosθdθ
=mgR2l|sinθ|l/R0=mgR2lsin(lR)
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Solved Examples
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
AS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.
View Solution
Knowledge Check
A chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The gravitational potential energy of the chain considering reference level at the base of hemisphere isA20 JB20√2JC40 JD40√2JA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The tangential acceleration of the chain when its starts sliding down.A40π(1−1√2)B20π(1−1√2)C10(1−1√2)DzeroA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
.A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
The total surface area of a hemisphere is 3768cm2. Find the radius of the hemisphere. (Take pi= 3.14)
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle θ=π4.
View Solution

