A worker wishes to pile a cone of sand onto a circular area in his yard. The radius of the circle is r,and no sand is to spill on to the surrounding area. If μ is the static coefficient of friction between each layer of sand along the slope and the sand, show that the greatest volume of sand that can be stored in this manner is 13πμR3.
Step by step video & image solution for A worker wishes to pile a cone of sand onto a circular area in his yard. The radius of the circle is r,and no sand is to spill on to the surrounding area. If mu is the static coefficient of friction between each layer of sand along the slope and the sand, show that the greatest volume of sand that can be stored in this manner is (1)/(3) pi muR^(3). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A worker wishes to pile up sand on to a circular area of radius R. No sand is to spill on to the surrounding area. If μs is the coefficient of static friction of sand on sand,the sand pile . Density of sand =ρ
View SolutionThe radius of the base of a right circular cone of semi-vertical angle α is r . Show that its volume is 13πr3 cotα and curved surface area is πr2 coses α.
View Solution
Knowledge Check
A worker wishes to pile up sand on to a circular area of radius R. No sand is to spill on to the surrounding area. If μs is the coefficient of static friction sand particles, then choose the correct statement (s)
AThe greatest height of sand pile that can be created is μsR.BThe greatest height of sand pile that can be created is R/μsCMinimum work required to create greatest height sand pile is π12μ2sR4ρg. Where ρ is the density of sand volumeDSand pile will be in stable equilibriumIf you want to pile up sand onto a circular area of radius R. The greatest height of the sand pile that can be created without spilling the sand onto the surrounding. Area, if μ is the coefficient of friction between sand particle is:
Aμ2RBμRCRDRμThe greatest height h of the sand pile that can be erected without spilling the sand onto the surrounding circular area of radius R (If μ is the coefficient of friction between sand particles) is
ARBRμCμRDμ2R
Sand is piled up on a horizontal ground in the form of a regualr cone of a fixed base of radius R.The coefficient of static friction between sand layers is μ.The maximum volume of sand that can be piled up, without the sand slipping on the surface is
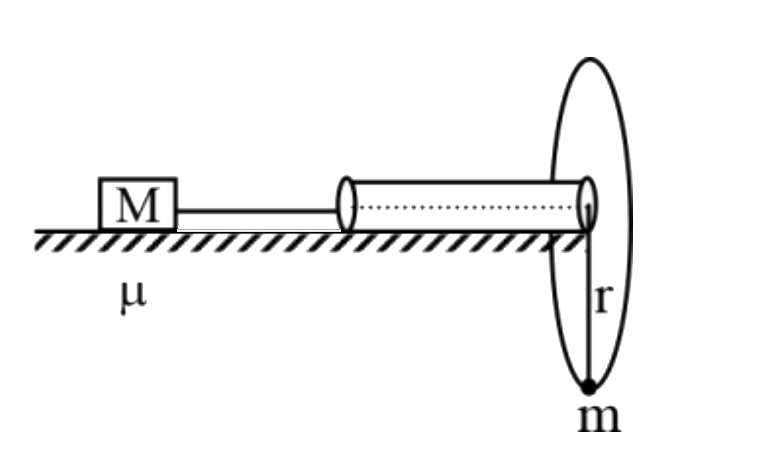
View SolutionThe figure below shows a block of mass M connected to an ideal string which passes through a thin fixed smooth pipe. On the other end, a particle of mass m is connected which revolves in a vertical circle of radius r. If the coefficient of friction between M and the surface is μ=23, then for what minimum value of M, the block of mass m can undergo complete vertical circular motion?
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−2m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?
View Solution
