The figure below shows a block of mass M connected to an ideal string which passes through a thin fixed smooth pipe. On the other end, a particle of mass m is connected which revolves in a vertical circle of radius r. If the coefficient of friction between M and the surface is μ=23, then for what minimum value of M, the block of mass m can undergo complete vertical circular motion?
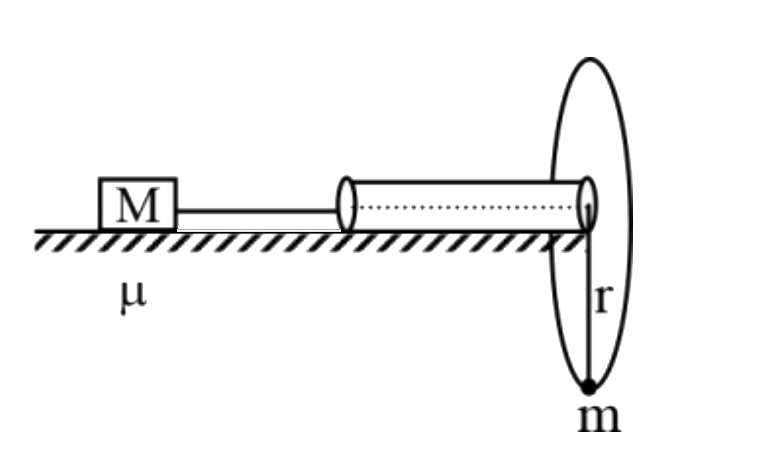
Mmin=6m
Mmin=9m
Mmin=3m
Mmin=15m
The correct Answer is:B
Step by step video, text & image solution for The figure below shows a block of mass M connected to an ideal string which passes through a thin fixed smooth pipe. On the other end, a particle of mass m is connected which revolves in a vertical circle of radius r. If the coefficient of friction between M and the surface is mu = 2/3, then for what minimum value of M, the block of mass m can undergo complete vertical circular motion? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
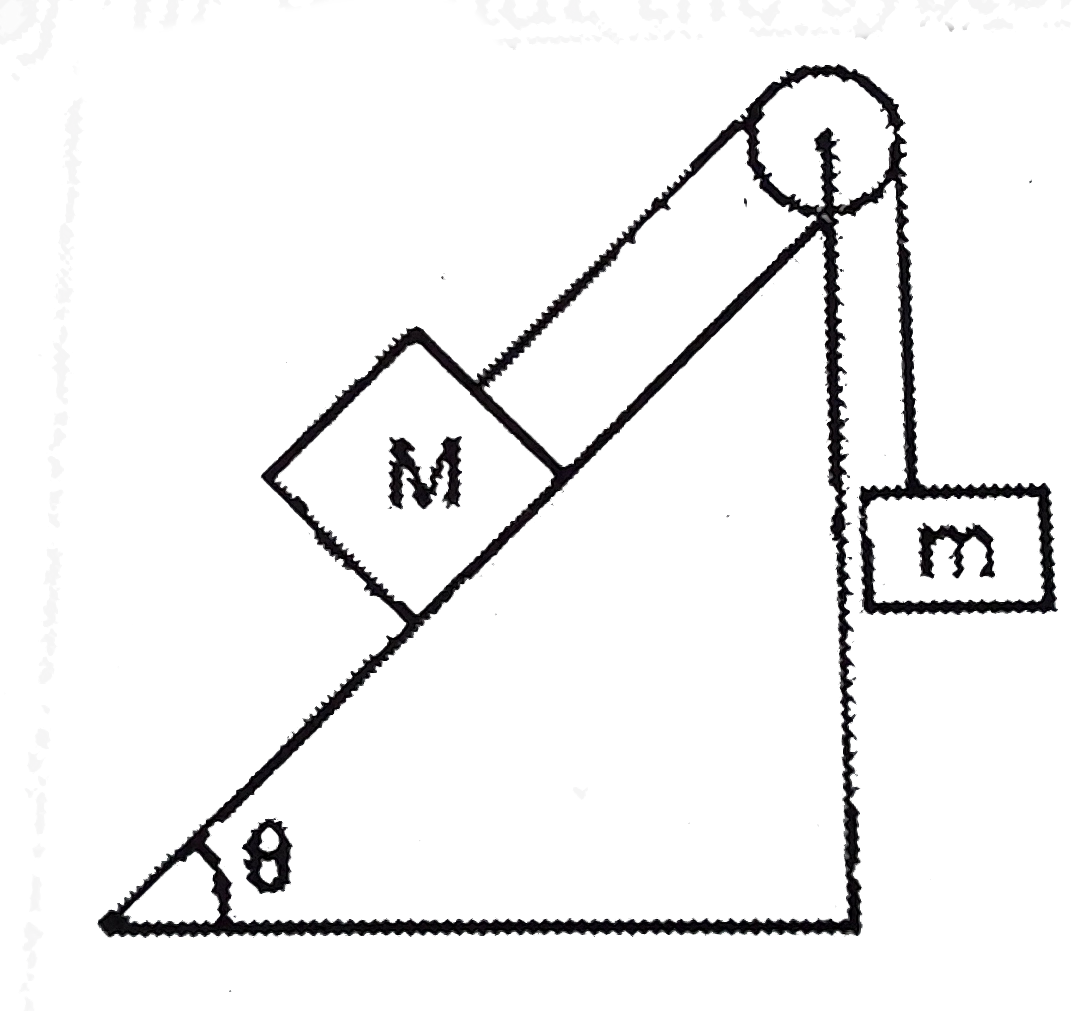
View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
View Solution
Knowledge Check
Coefficient of friction between block of mass m and fixed wedge is μ=0.5. For what value of mM frictional force between block of mass m and wedge becomes zero ?
 A12B2C1DNone of these
A12B2C1DNone of theseA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?
 AμgBg/μCμ/gDMμg/m
AμgBg/μCμ/gDMμg/mTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?
 AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
AM2=M1(sinθ+μcosθ)BM2=M1(sinθ−μcosθ)CM2=M1sinθ+μcosθDM2=M1sinθ−μcosθ
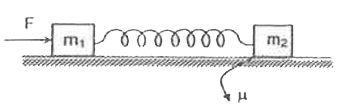
Two blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View SolutionA block of mass m is stationary on a horizontal surface. It is connected with a string which has no tension. The coefficient of friction between the block and surface is m . Then , the frictional force between the block and surface is:

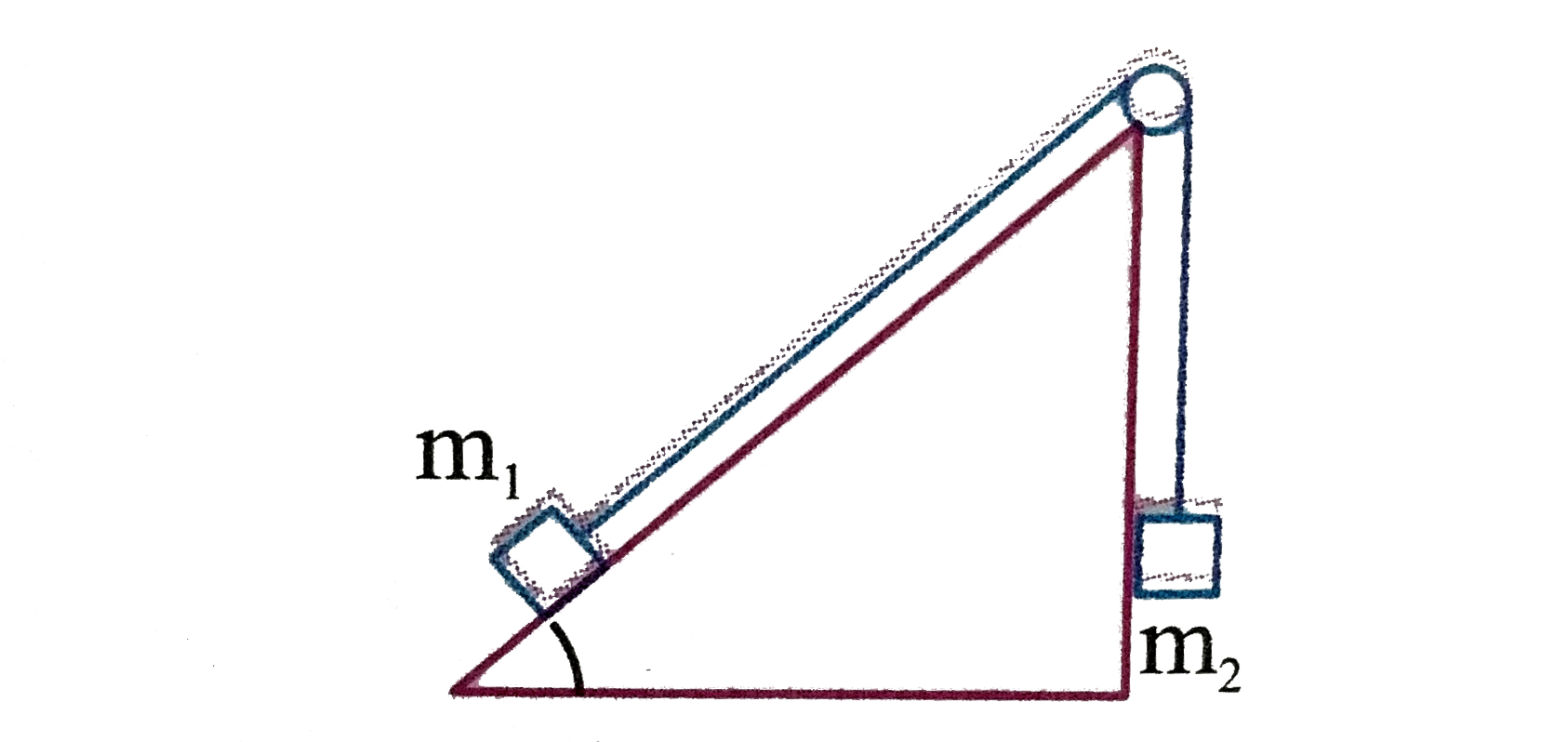
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View Solution