A thin uniform equilateral plate rests in a vertical plane with one of its vertex A on a rough horizontal floor and another vertex B on a smooth vertical wall. If the coefficient of friction μ=1√3, then the least angle θ its base AB can make with the horizontal surface is
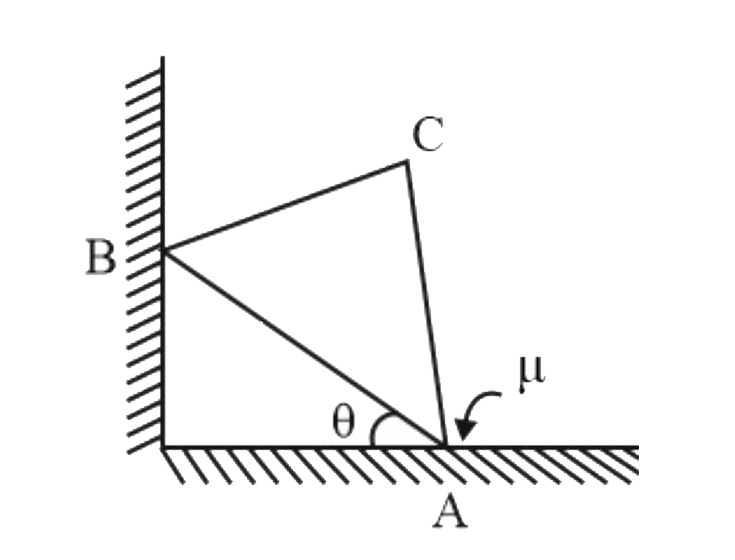
θ=cot−1[μ+1√3]
θ=tan−1[μ+1√3]
θ=tan−1[2μ+1√3]
θ=cot−1[2μ+1√3]
The correct Answer is:D
Step by step video, text & image solution for A thin uniform equilateral plate rests in a vertical plane with one of its vertex A on a rough horizontal floor and another vertex B on a smooth vertical wall. If the coefficient of friction mu = 1/(sqrt3), then the least angle theta its base AB can make with the horizontal surface is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A solid homigeneous hemisphere rests on a rough horizontal plane and against a smooth vertical wall. If the coefficient of friction is greater than 38, the hemisphere can rest in any position and if it is less, the least angle that the base of the hemisphere can make with the vertical is cos−1(8μ3). If the wall be rough, the coefficient of friction μ, this angle is cos−1(8μ3.1+μ'1+μμ') .
View SolutionA body of mass 10 kg slides a long a rough horizontal surfce. The coefficient of friction is 1/√3. Taking g=10m/s2. The least force which acts at an angle of 30∘ to the horizontal is
View Solution
Knowledge Check
A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)A uniform ladder rests in limiting equilibrium, its lower end on a rough horizontal plae and its upper end against a smooth vertical wall. If θ is the engle of inclination of the ladder to the vertical wall and μ is the coefficient of friction then tanθ is equal to
AμB2μC3μ/2Dμ+1
A uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View SolutionA mass of 100kg is resting on a rough inclined plane of angle 30∘ If the coefficient of friction is 1/√3 find the greatest and the least forces that acting parallel to the plane in both cases just maintain the mass in equilibrium .
View SolutionA ladder whose centre of gravity divides its length in the ratio a : b is in limting equilibrium with its one end on a rough floor (coefficient of friction μ) and the other end against a rough vertical wall (coefficient of friction μ) .Determine the angle of inclination of the ladder in terms of two angles of friction .
View SolutionA block of weight 100N is lying on a rough horizontal surface.If coefficient of friction 1√3.The least possible force that can move the block is
View SolutionA steel ball strikes a fixed smooth steel plate placed on a horizontal surface at an angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
View Solution

