Two long coaxial solenoids of radius R and 2R have equal number of turns per unit length. They carry time-varying currents. i1=2ktandi2=kt respectively, in the same direction. A point charge released between the solenoids at a distance r, is seen to move along a circular path. Then the value of r is
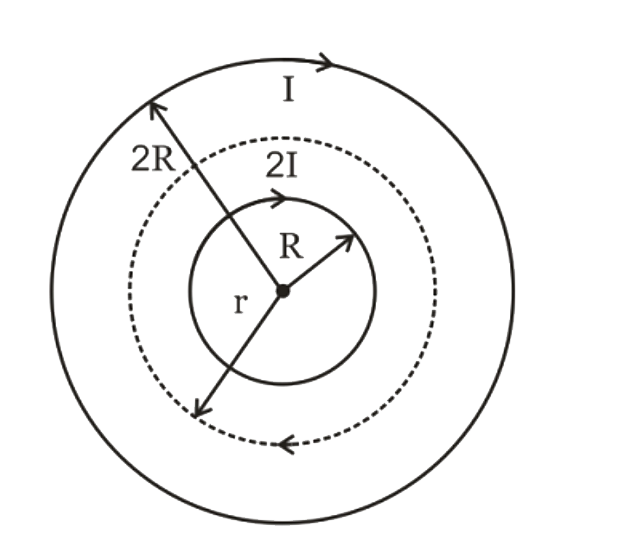
r=R√2
r=3R/2
r=R√3
It can be any value between Rand2R
The correct Answer is:A
Step by step video, text & image solution for Two long coaxial solenoids of radius R and 2R have equal number of turns per unit length. They carry time-varying currents. i_(1) = 2 kt and i_(2) = kt respectively, in the same direction. A point charge released between the solenoids at a distance r, is seen to move along a circular path. Then the value of r is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
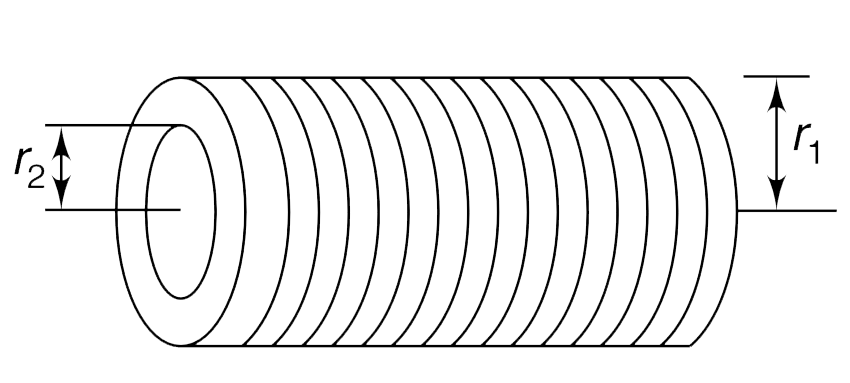
Two long co-axial solenoids have radii, and number of turns per unit length equal to r1,r2 and n1,n2 respectively where suffix 1 refers to the outer solenoid and 2 refers to the inner solenoid. Length of both is l. The current in the outer solenoid is made to grow as I1=kt where t is time. Resistance of the wire used in inner solenoid is R. Write the current induced in the inner solenoid assuming that it is shorted.
View SolutionTwo coaxial circular loops of raadii r1 and r2 are separated by a distance x and carry currents i1 and i2 respectively. Calculate the mutual inductance. What is the force between the loops ?
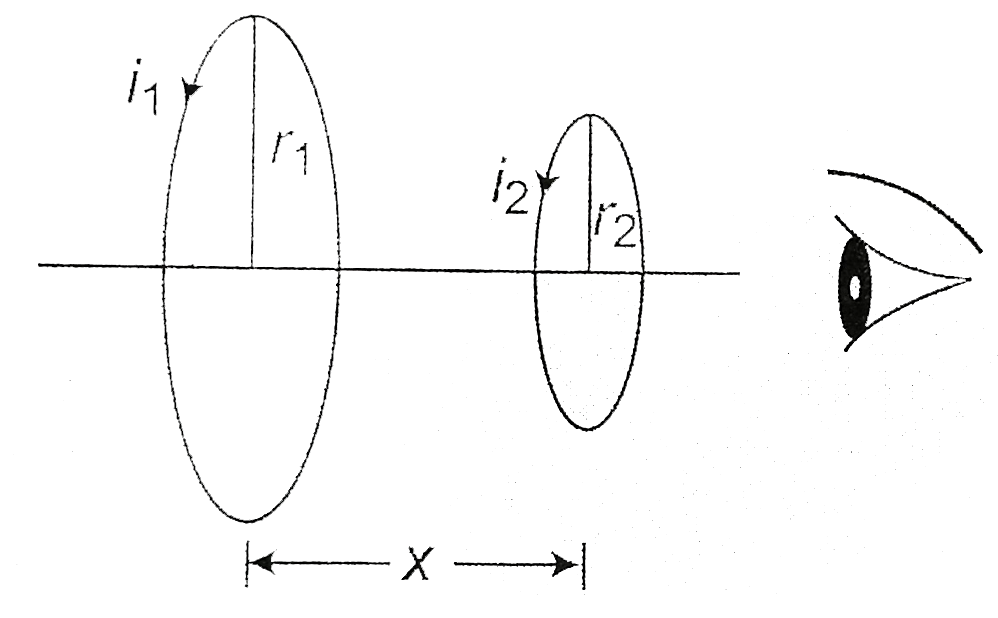
View Solution
Knowledge Check
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
AaniBniCniaDn2iA long solenoid of radius 2R contains another coaxial solenoid of radius R. The coils have the same number of turns per unit length and initially both carry zero current. At time, t=0, current start increasing linearly with time in both solenoids. At any moment the current flowing in the inner coil is twice as large as that in the outer one and their directions are same. A charged particle, initially at rest between the two solenoids, start moving along a circular trajectory due to increasing current in the solenoid as shown in the figure What is the radius of the circle ? (Assume magnetic field due to each solenoid remains uniform over its cross-section.)
 A√2RB√3RC32RDnone of these
A√2RB√3RC32RDnone of theseA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
Aμ0nI0ωR22rsinωtBμ0nI0ωR2rsinωtCμ0nI0R22rsinωtDzero
There are two long co-axial solenoids of same length l. The inner and other coils have redii r1 and r2 and number of turns per unti length n1 and n2 respectively .The reatio of mutual inductance to the self - inductance of the inner- coil is :
View SolutionTwo parallel coaxial circular coils of equal radius R and equal number of turns N carry equal currents I in the same direction and are separated by a distance 2R. Find the magnitude and direction of the net magnetic field produced at the mid-point of the line joining their centres.
View SolutionThe current in a long solenoid of radius R and having n turns per unit length is given by i=i0sinωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
View SolutionTwo coaxil solenoids 1 and 2 of the same length are set so that one is inside the other. The number of turns per unit length are n1 and n2. The current i1 and i2 are flowing in opposite directions. The magnetic field inside the inner coil is zero. This is possible when
View SolutionTwo coaxial solenoids having same number of turns per unit length n, and radius R and 2R respectively have no current initially. Current in both grows uniformly such that current in the inner one is twice that of the outer one, at any instant of time in the same direction. Current in outer one at time t is Kt then induced electric field at a distance r from axis is (R<r<2R).
View Solution

