Two coaxial circular loops of raadii r1 and r2 are separated by a distance x and carry currents i1 and i2 respectively. Calculate the mutual inductance. What is the force between the loops ? 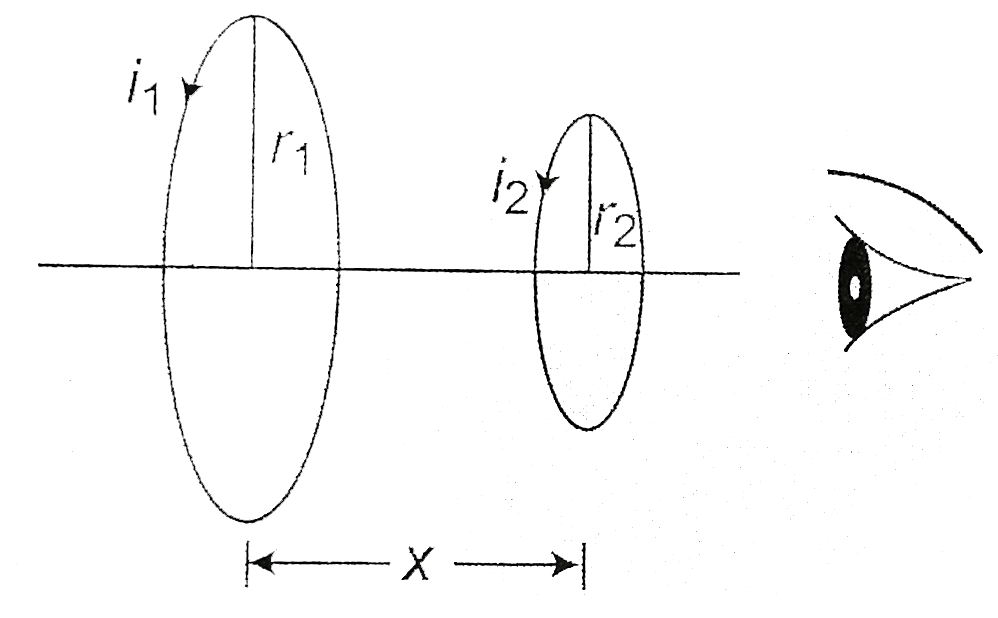
Magnetic field due to loop (1) at (2)
B1=μ0i1r212(r21+x2)3/2 , along the axis
Flux passing through (2)
ϕ=B1A2=μ0i1r212(r21+x2)3/2πr22
Mutual inductance
M=ϕ2i1=μ0πr21r222(r21+x2)3/2
Magnetic moment of loop (2)
M2=i2.πr22 , along the axis
P.E. of loop (2) ltbr> U=−→M2.→M1=−M2B1=−i2πr22μ0i1r212(r2+x2)3/2
F=−dUdx=μ0i1i2πr21r222(−32)(r2+x2)−5/2(2x)
=−3μ0i1i2πr21r22x2(r2+x2)5/2
−ve sign shows that foorce is attractive.
Topper's Solved these Questions
Similar Questions
Two circular loops A and B of radii R and 4R are kept concentrically in the same plane. The loops carry currents I1 and I2 respectively. If the magnetic field at a point on the common axis of the loops at a distance 2R from their common centre is zero, the ratio I1I2 is _________.
View SolutionTwo circular loops of radii R and r (R > > r) have same cenre and carry currents I and i respectively. Find the maximum torque and maximum angular acceleration of smallar loop, if it is free to rotate about y axis where as the bigger loop is fixed. (Neglect the inductance of the system). The mas of the smaller loop is m.

View Solution
Knowledge Check
Two coaxial circular loops of radius 0.5m and 5×10−2m are separated by a distance 0.5m and carry currents 2A and 1A respectively. The force between the loops due to mutual induction is
 A2.09×10−8NB1.06×10−6NC4.18×10−8ND8.3×10−5N
A2.09×10−8NB1.06×10−6NC4.18×10−8ND8.3×10−5NTwo concentric circular loops of radiir1 and r2 carry clockwise and anticlockwise currents i1 and i2. If the centre is a null point, i1/i2 must be equal to
Ar2/r1Br22/r21Cr21/r22Dr1/r2Two concentric coplanar circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to i1 alone at the centre. if r2=2r1. the value of i2/i1 is
A2B1/2C1/4D1
Two concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo conducting circular loops of radii R1 and R2 are placed in the same plane with their centres coinciding. If R1 >> R2 the mutual inductance M between them will be directly proportional to
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
View SolutionA circular loop of radius r is placed at the center of current carrying conducting square loop of side a. If both loops are coplanar and a >> r, then the mutual inductance between the loops will be
View SolutionTwo circular coils P & Q are coaxially & carry currents I1 and I2 respectively (all direction are w.r.t. the observer)

View Solution
