A block m= 0.5kg slides down a frictionless inclined plane 2 m long as showi in figure-2.196. It then slides on a rough horizontal table surface of μ=0.3 for 0.5 m. It then leaves the top of the table,which is 1.0 m high. How far from the base of the table does the block land ?
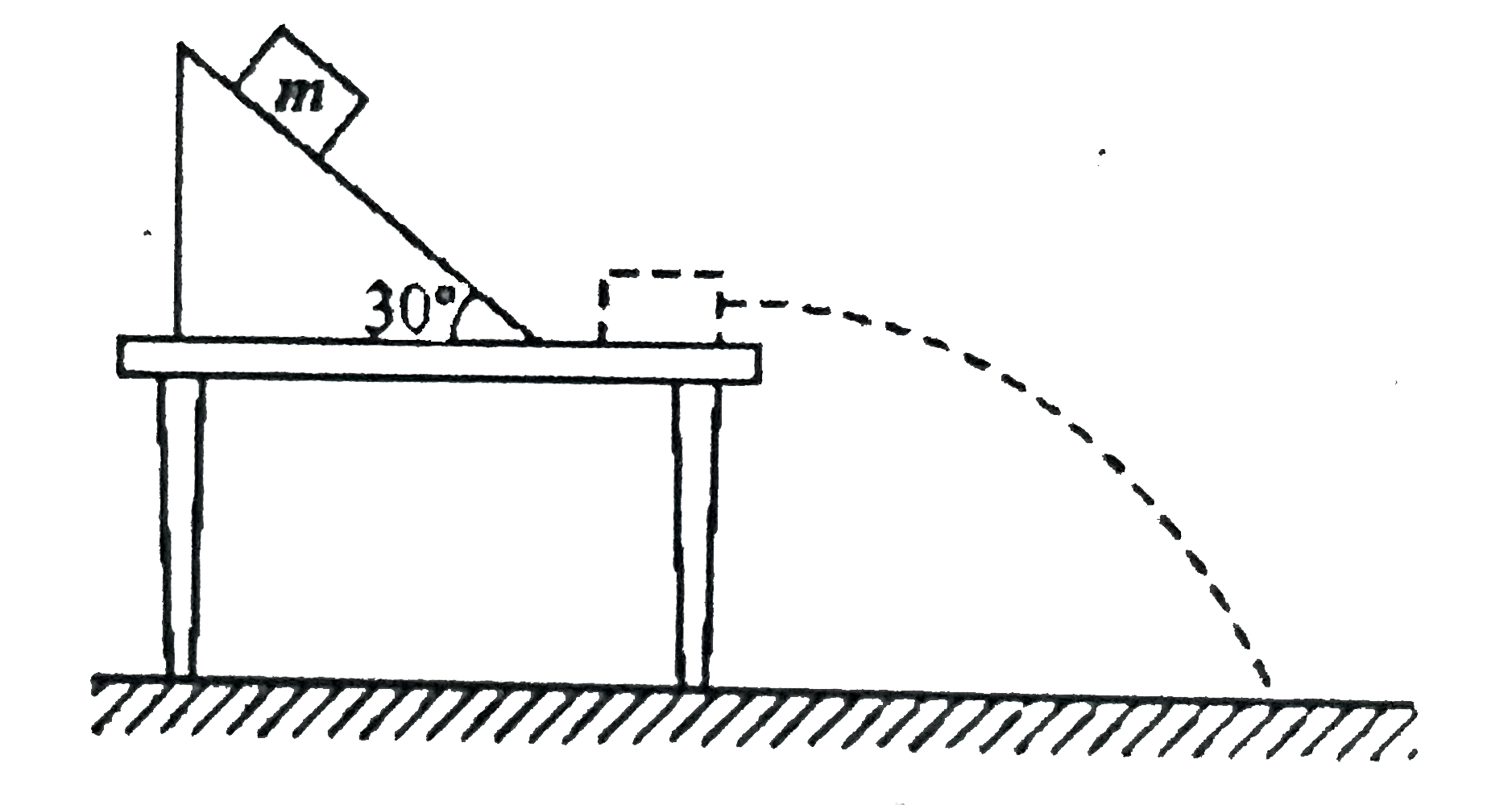
The correct Answer is:[1.85 m]
Step by step video, text & image solution for A block m= 0.5kg slides down a frictionless inclined plane 2 m long as showi in figure-2.196. It then slides on a rough horizontal table surface of mu = 0.3 for 0.5 m. It then leaves the top of the table,which is 1.0 m high. How far from the base of the table does the block land ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Advance MCQs
17 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A block of mass 5.0 kg slides down an incline of inclination 300 and length 10 m. The work done by the force of gravity (in joule) is
View Solution1 kg particle at a height of 4 m has a speed of 2 m/s down a incline making an angle 53∘ with horizontal as shown in figure. It slides on a horizontal section of length 3 m at ground level and then up an incline making an angle 37∘ with horizontal. All surfaces have μk=0.5. How far from point O (bottom of right inclined plane), along the incline making and angle 37∘ with horizontal, does the particle first come to rest?
View Solution
Knowledge Check
A massless string and a spring connect two blocks A and B to each other. Block B slides over a frictionless inclined plane while block A slides over horizontal surface. Coefficient of friction between block a A horizontal surface is μ=0.2. At the instant shown blocks are moving with constant speed. Mass of block A and energy stored in spring the respectively. [g=10m/s2,k=1000Nm,mB=2kg]
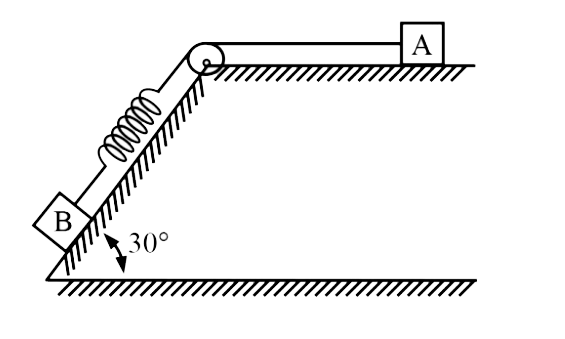 A5 kg, 1JB10 kg, 0.05 JC5 kg, 0.05 JD10 kg, 1J
A5 kg, 1JB10 kg, 0.05 JC5 kg, 0.05 JD10 kg, 1JA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
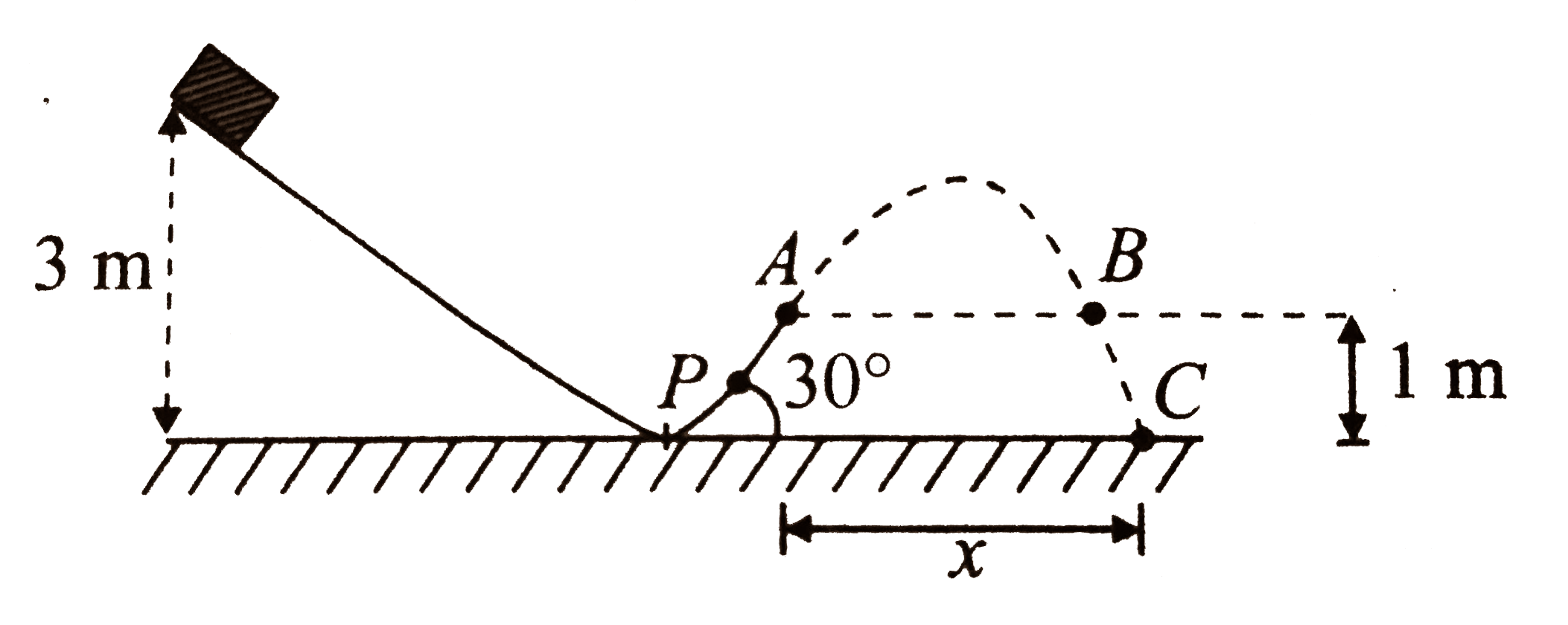 .
.
The horizontal distance x travelled by the block in moving from A to C is.A(1+√3)mB(1−√3)mC(√3+3))mDg meterA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
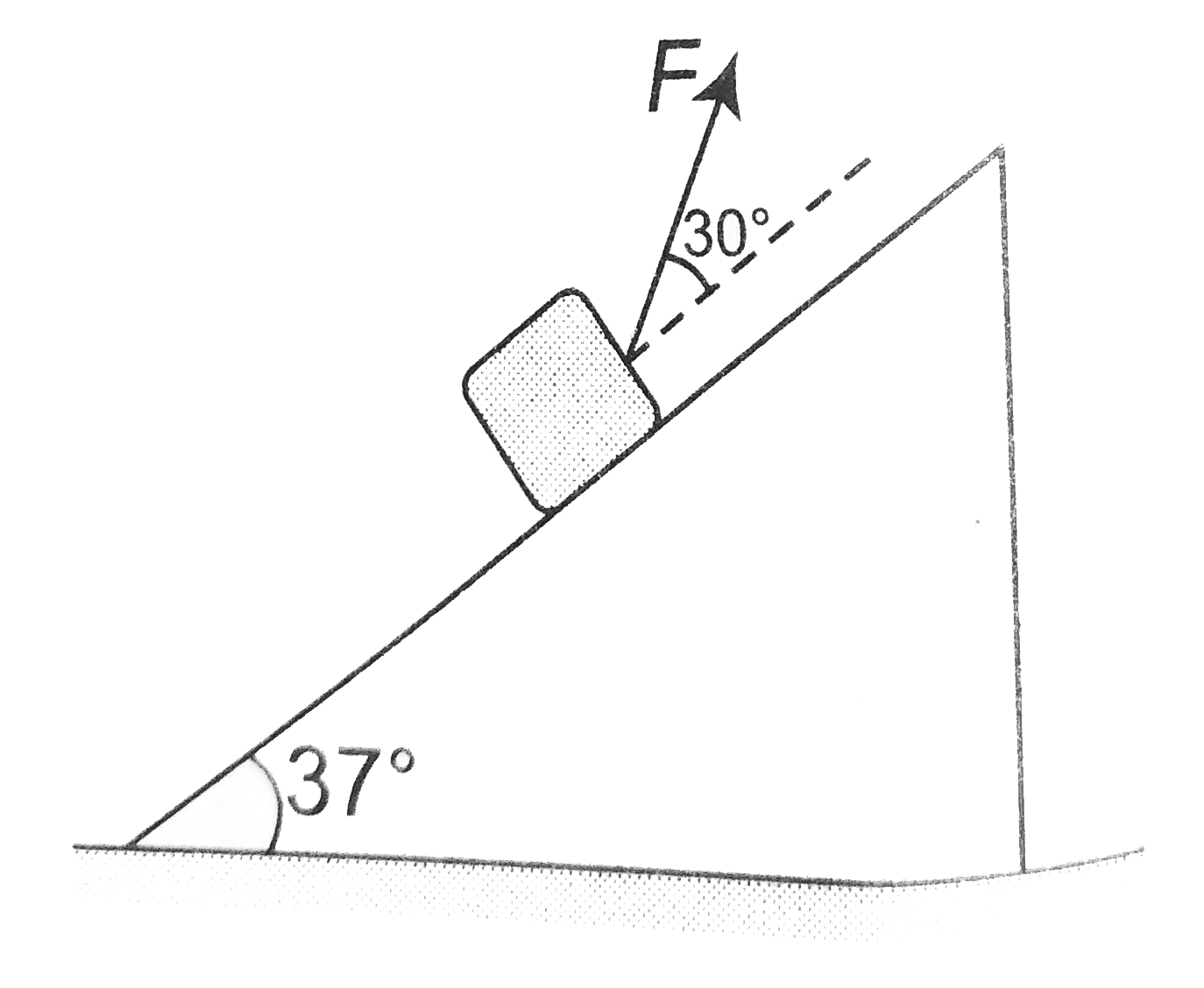 Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these
Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these
A block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block
View SolutionA block of mass 250 g slides down an incline of inclination 370 with a uniform speed. Find the work done against the friction as the block slides through 1.0 m.
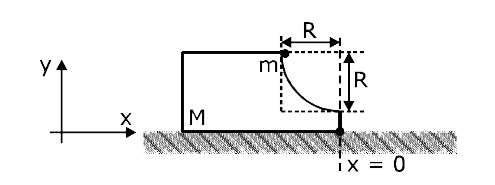
View SolutionA block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
View SolutionA block of weight 15N slides on a horizontal table the co-efficient of siliding fricition is 0.4. The area of the block in contact with the table is 0.5m2. The shearing stress will be
View SolutionA block mass 'm' is placed on a frictionless inclined plane of inclination θ with horizontal. The inclined plane is accelerated horizontally so that the block does not slide down. In this situation vertical force exerted by the inclined plane on the block is:
View Solution
