Two identical beads each of mass 'm' can slide freely on a ring of mass M lying on smooth horizontal surface. The masses are brought to diametrically opposite positions and both are imparted with same tangential speed v in same direction. Find the kinetic energy of the ring when beads are about to collide.
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have two identical beads each of mass m on a ring of mass M. The beads are initially at diametrically opposite positions on the ring and are given the same tangential speed v in the same direction.
Step 2: Analyze Initial Momentum
Initially, the total momentum of the system (both beads and the ring) is given by:
Pinitial=mv+mv=2mv
The ring is initially at rest, so its initial momentum is zero.
Step 3: Apply Conservation of Momentum
Since there are no external forces acting on the system, the total momentum of the system must be conserved. Let Vr be the final velocity of the ring when the beads are about to collide. The final momentum of the system can be expressed as:
Pfinal=2mVb+MVr
where Vb is the final velocity of the beads.
Step 4: Determine the Final Velocities
When the beads are about to collide, they will have some velocity Vb in the direction of their initial motion. The momentum conservation equation becomes:
2mv=2mVb+MVr
Step 5: Relate the Velocities of Beads and Ring
Since the beads are moving on the ring, their motion will affect the ring's motion. The beads will exert a force on the ring, causing it to move. By symmetry and conservation of momentum, we can assume:
Vb=Vr
Thus, we can rewrite the momentum conservation equation as:
2mv=2mVr+MVr
Step 6: Solve for the Ring's Velocity
Rearranging the momentum equation gives:
2mv=Vr(2m+M)
Solving for Vr:
Vr=2mv2m+M
Step 7: Calculate the Kinetic Energy of the Ring
The kinetic energy KE of the ring is given by:
KE=12MV2r
Substituting Vr from the previous step:
KE=12M(2mv2m+M)2
Calculating this gives:
KE=12M⋅4m2v2(2m+M)2
KE=2Mm2v2(2m+M)2
Final Answer
The kinetic energy of the ring when the beads are about to collide is:
KE=2Mm2v2(2m+M)2
---
We have two identical beads each of mass m on a ring of mass M. The beads are initially at diametrically opposite positions on the ring and are given the same tangential speed v in the same direction.
Initially, the total momentum of the system (both beads and the ring) is given by:
Pinitial=mv+mv=2mv
The ring is initially at rest, so its initial momentum is zero.
Since there are no external forces acting on the system, the total momentum of the system must be conserved. Let Vr be the final velocity of the ring when the beads are about to collide. The final momentum of the system can be expressed as:
Pfinal=2mVb+MVr
where Vb is the final velocity of the beads.
When the beads are about to collide, they will have some velocity Vb in the direction of their initial motion. The momentum conservation equation becomes:
2mv=2mVb+MVr
Since the beads are moving on the ring, their motion will affect the ring's motion. The beads will exert a force on the ring, causing it to move. By symmetry and conservation of momentum, we can assume:
Vb=Vr
Thus, we can rewrite the momentum conservation equation as:
2mv=2mVr+MVr
Rearranging the momentum equation gives:
2mv=Vr(2m+M)
Solving for Vr:
Vr=2mv2m+M
The kinetic energy KE of the ring is given by:
KE=12MV2r
Substituting Vr from the previous step:
KE=12M(2mv2m+M)2
Calculating this gives:
KE=12M⋅4m2v2(2m+M)2
KE=2Mm2v2(2m+M)2
The kinetic energy of the ring when the beads are about to collide is:
KE=2Mm2v2(2m+M)2
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I
Explore 45 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)
Explore 2 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Numerical)
Explore 8 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionAngular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View Solution
Knowledge Check
A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A1/2Mv2B3/2Mv2CMv2D1/2MR2ω2A ring and a disc roll on the horizontal surface without slipping with same linear velocity. If both have same mass and total kinetic energy of the ring is 4 J then total kinetic energy of the disc is
A3 JB4 JC5 JD6 JA ring and a disc roll on the horizontal surface without slipping with same linear velocity. If both have same mass and total kinetic energy of the ring is 4 J then total kinetic energy of the disc is
A3 JB4 JC5 JD6 J
Angular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View SolutionA hollow smooth uniform A of mass 'm' rolls without sliding on a smooth horizontal surface collides head to elastically with another stationary smooth solid sphere B of the same mass m and same radius. The ratio of kinetic energy of 'B' to that of 'A' just after the collision is -
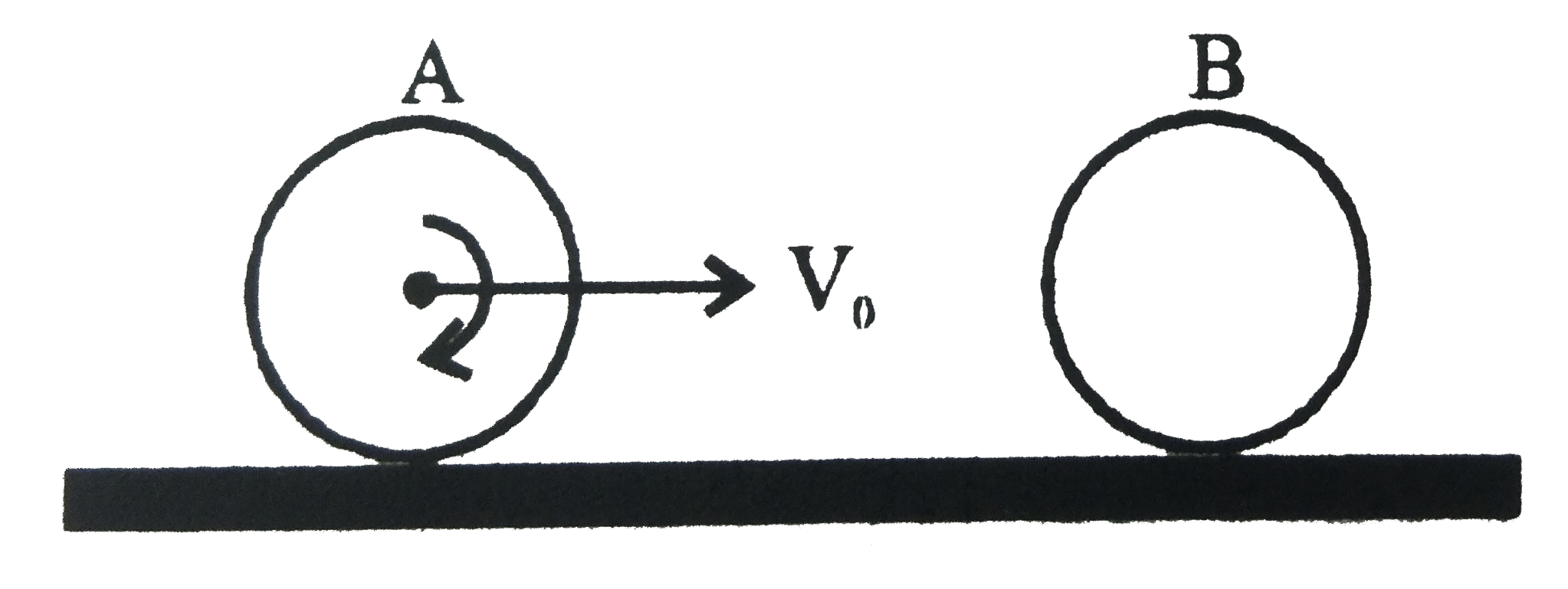 .
.
View SolutionA ring and a disc roll on the horizontal surface without slipping, with same linear velocity. If bolh have same mass and total kinetic energy of the ring is 4 J, then total kinetic energy of the disc is
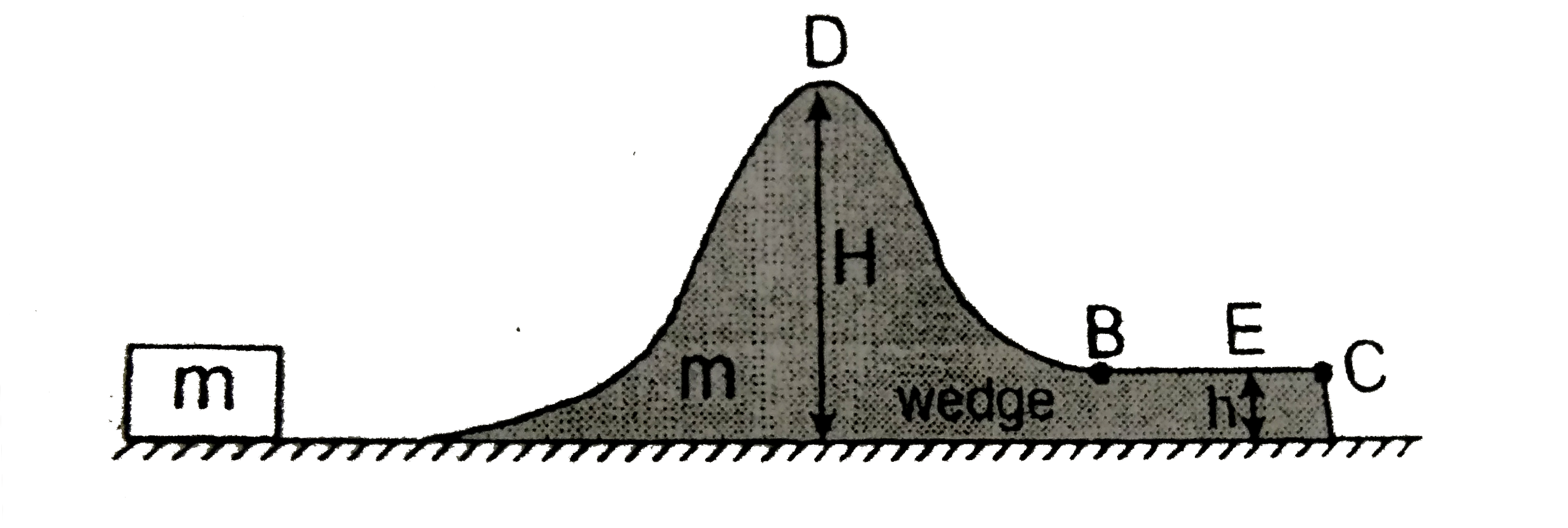
View SolutionFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
What minimum velocity should be imparted to a small block of same mass m so that it may each point B :
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View Solution