Question

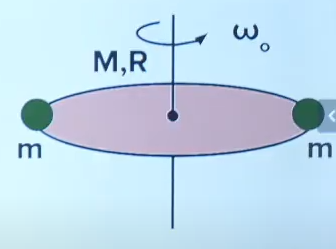
Angular velocity of a ring is $\omega$. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)

Answer

` omega' = omega/3 `

Explanation

To solve the problem of finding the resultant angular velocity of a ring with two masses added at diametrically opposite points, we can follow these steps:

1. Understand the System:
We have a ring with an initial angular velocity \( \omega \) and a mass \( m \). Two additional masses, each of mass \( m \), are placed at diametrically opposite points on the ring.

2. Identify the Moment of Inertia:
The moment of inertia \( I \) of a ring about its center is given by:
\( I_{\text{ring}} = m R^2 \)
where \( R \) is the radius of the ring.

3. Calculate the Moment of Inertia of the Added Masses:
Each mass \( m \) is located at a distance \( R \) from the center of the ring. Since there are two masses, the total moment of inertia contributed by the two masses is:
\( I_{\text{masses}} = 2 \cdot m R^2 = 2m R^2 \)

4. Total Moment of Inertia:
The total moment of inertia \( I_{\text{total}} \) of the system (ring + two masses) is:
\( I_{\text{total}} = I_{\text{ring}} + I_{\text{masses}} = m R^2 + 2m R^2 = 3m R^2 \)

5. Apply Conservation of Angular Momentum:
According to the conservation of angular momentum, the initial angular momentum \( L_i \) must equal the final angular momentum \( L_f \):
\( L_i = I_{\text{ring}} \cdot \omega = m R^2 \cdot \omega \)
\( L_f = I_{\text{total}} \cdot \omega' = 3m R^2 \cdot \omega' \)
Setting these equal gives:
\( m R^2 \cdot \omega = 3m R^2 \cdot \omega' \)

6. Solve for the Resultant Angular Velocity \( \omega' \):
Dividing both sides by \( m R^2 \) (assuming \( m \neq 0 \) and \( R \neq 0 \)):
\( \omega = 3 \omega' \)
Rearranging gives:
\( \omega' = \frac{\omega}{3} \)

Final Result:
The resultant angular velocity \( \omega' \) of the ring after adding the two masses is:
\( \omega' = \frac{\omega}{3} \)