The coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhere to the wall will be ____N.
The correct Answer is:25
To solve the problem, we need to determine the magnitude of the horizontal force (F) that should be applied on a wooden block of mass 0.5 kg to keep it adhered to a vertical rough wall, given that the coefficient of static friction (μ) between the block and the wall is 0.2.
1. Identify the forces acting on the block:
- The weight of the block (W) acting downwards:
W=mg
where m=0.5kg and g=10m/s2.
- The normal force (N) acting perpendicular to the wall, which is equal to the applied horizontal force (F).
- The frictional force (f) acting upwards, which opposes the weight of the block.
2. Calculate the weight of the block:
W=mg=0.5kg×10m/s2=5N
3. Determine the frictional force:
The maximum static frictional force can be calculated using the formula:
f=μN
where μ=0.2.
4. Set up the equilibrium condition:
For the block to remain at rest, the upward frictional force must balance the downward weight:
f=W
Substituting the expression for friction:
μN=mg
5. Substituting the normal force:
Since the normal force N is equal to the applied horizontal force F:
μF=mg
6. Rearranging the equation to find F:
F=mgμ
7. Substituting the known values:
F=5N0.2=25N
Final Answer:
The magnitude of the horizontal force that should be applied on the block to keep it adhered to the wall is 25 N.
- The weight of the block (W) acting downwards:
W=mg
where m=0.5kg and g=10m/s2.
- The normal force (N) acting perpendicular to the wall, which is equal to the applied horizontal force (F).
- The frictional force (f) acting upwards, which opposes the weight of the block.
W=mg=0.5kg×10m/s2=5N
The maximum static frictional force can be calculated using the formula:
f=μN
where μ=0.2.
For the block to remain at rest, the upward frictional force must balance the downward weight:
f=W
Substituting the expression for friction:
μN=mg
Since the normal force N is equal to the applied horizontal force F:
μF=mg
F=mgμ
F=5N0.2=25N
The magnitude of the horizontal force that should be applied on the block to keep it adhered to the wall is 25 N.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-A)
20 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION-B)
10 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionIn the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
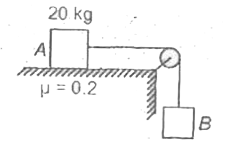
View Solution
Knowledge Check
Consider the arrangement shown in the figure. The coefficient of friction between the two blocks is 0.5 and between the 4 kg block and the horizontal surface is 0.4. If a horizontal force of 12 N is applied on the 4 kg block, the acceleration of the 2 kg block would be
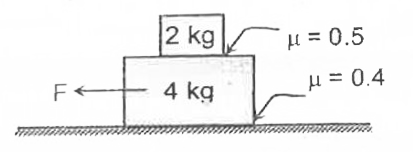 A2.5m/s2B2m/s2C5m/s2Dzero
A2.5m/s2B2m/s2C5m/s2DzeroA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
A8.8NB5.8NC2.8ND10.8NA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
A8.8 NB5.8 NC2.8 ND10.8 N
A block weighing 20 N rests on a horizontal surface. The: coefficient of static friction between block and surface is 0.40 and the coefficient of kinetic friction is 0.20.
( a) How large is the friction force exerted on the block?
(b) How great will the friction force be if a horizontal force of 5 N is exerted on the block?
(c) What is the minimum force that will start the block in motion?
(d) What is the minimum force that will keep the block in motion once it has been started?
(e) If the horizontal force is 10 N, what is the friction force?
View Solution(i) In the arrangement shown in the figure the coefficient of friction between the 2 kg block and the vertical wall is μ=0.5. A constant horizontal force of 40 N keeps the block pressed against the wall. The spring has a natural length of 1.0 m and its force constant is k=400Nm–1. What should be the height h of the block above the horizontal floor for it to be in equilibrium. The spring is not tied to the block.
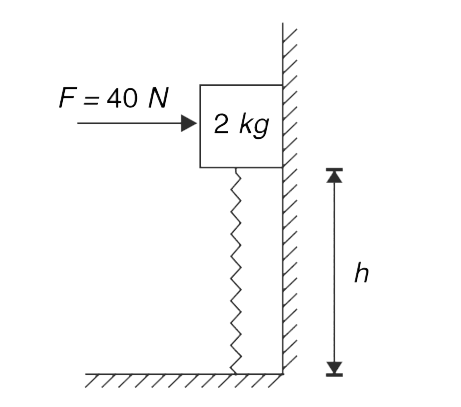
(ii) A block of mass M is pressed against a rough vertical wall by applying a force F making an angle of θ with horizontal (as shown in figure). Coefficient of friction between the wall and the block is μ=0.75.
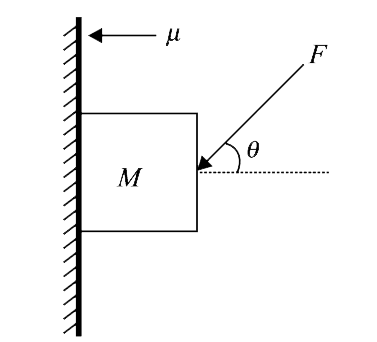
(a) If F = 2 Mg, find the range of values of θ so that the block does not slide
[Take tan37∘=0.75,sin24∘=0.4]
(b) Find the maximum value of θ above which equilibrium is not possible for any magnitude of force F.
View SolutionA block of mass 1kg is at rest on a horizontal table. The coefficient of static friction between the block and the table is 0.5 . The magnitude of the force acting upward at an angle of 60∘ from the horizontal that will just start the block moving is.
View SolutionA block of mass 70 kg is kept on a rough horizontal surface and coefficient of static friction between block and surface is 0.4 . A man is trying to pull the block by applying a horizontal force .The net contact force exerted by the surface on the block is F , then:
View SolutionA block of mass 2kg is held at rest against a rough vertical wall by passing a horizontal (normal) force of 45N. Coefficient of friction between wall and the block is equal to 0.5. Now a horizontal force of 15N (tangential to wall) is also applied on the block. Then the block will :
View Solution
