A block of mass 1kg is at rest on a horizontal table. The coefficient of static friction between the block and the table is 0.5 . The magnitude of the force acting upward at an angle of 60∘ from the horizontal that will just start the block moving is.
5N
202+√3N
202−√3N
10N
The correct Answer is:B
To solve the problem step by step, we will analyze the forces acting on the block and apply Newton's laws of motion.
Step 1: Identify the forces acting on the block
The forces acting on the block are:
1. The weight of the block (W = mg) acting downwards.
2. The normal force (R) acting upwards.
3. The applied force (F) acting at an angle of 60 degrees above the horizontal.
Step 2: Break down the applied force into components
The applied force F can be broken down into two components:
- Horizontal component: Fx=Fcos(60∘)=F2
- Vertical component: Fy=Fsin(60∘)=F√32
Step 3: Write the equations for equilibrium
Since the block is at rest initially, we can use the equilibrium conditions:
1. In the vertical direction (y-direction):
R+Fy=W
Substituting the values:
R+F√32=mg
Where m=1kg and g=10m/s2:
R+F√32=10
Rearranging gives:
R=10−F√32(Equation 1)
2. In the horizontal direction (x-direction):
The frictional force Ff that opposes the motion is given by:
Ff=μR
Where μ=0.5. The equation for the horizontal forces becomes:
Fx=Ff
Substituting the values:
Fcos(60∘)=μR
Which simplifies to:
F2=0.5R
Rearranging gives:
F=R(Equation 2)
Step 4: Substitute Equation 1 into Equation 2
Substituting the expression for R from Equation 1 into Equation 2:
F=10−F√32
Rearranging gives:
F+F√32=10
Factoring out F:
F(1+√32)=10
Thus,
F=101+√32
Step 5: Simplify the expression for F
To simplify:
F=102+√32=202+√3
Final Answer
The magnitude of the force acting upward at an angle of 60∘ that will just start the block moving is:
F=202+√3N
The forces acting on the block are:
1. The weight of the block (W = mg) acting downwards.
2. The normal force (R) acting upwards.
3. The applied force (F) acting at an angle of 60 degrees above the horizontal.
The applied force F can be broken down into two components:
- Horizontal component: Fx=Fcos(60∘)=F2
- Vertical component: Fy=Fsin(60∘)=F√32
Since the block is at rest initially, we can use the equilibrium conditions:
1. In the vertical direction (y-direction):
R+Fy=W
Substituting the values:
R+F√32=mg
Where m=1kg and g=10m/s2:
R+F√32=10
Rearranging gives:
R=10−F√32(Equation 1)
The frictional force Ff that opposes the motion is given by:
Ff=μR
Where μ=0.5. The equation for the horizontal forces becomes:
Fx=Ff
Substituting the values:
Fcos(60∘)=μR
Which simplifies to:
F2=0.5R
Rearranging gives:
F=R(Equation 2)
Substituting the expression for R from Equation 1 into Equation 2:
F=10−F√32
Rearranging gives:
F+F√32=10
Factoring out F:
F(1+√32)=10
Thus,
F=101+√32
To simplify:
F=102+√32=202+√3
The magnitude of the force acting upward at an angle of 60∘ that will just start the block moving is:
F=202+√3N
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Problems Based On Mixed Concepts
Explore 51 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Applications Of Newton'S Laws Of Motion
Explore 33 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .
.
View SolutionIn Fig. 6-37, a block of mass m = 5.0 kg is at rest on a ramp. The coefficient of static friction between the block and ramp is not known. Find the magnitude of the net force exerted by the ramp on the block.

View Solution
Knowledge Check
A block weighing 10kg is at rest on a horizontal table. The coefficient of static friction between the block and the table is 0.5. If a force acts downward at 60∘ with the horizontal, how large can it be without causing the block to move ? (g=10ms−2)
A346 NB446 NC746 ND846 NA block weighing 10kg is at rest on a horizontal table. The coefficient of static friction between the block and the table is 0.5. If a force acts downward at 60∘ with the horizontal, how large can it be without causing the block to move ? .(g=100ms−2) .
A346NB446NC746ND846NA block of mass 5 kg is placed on a rough horizontal plane. The coefficient of static and kinetic friction between the block and surface is 0.5 and 0.3 respectively. A force of 100 N is applied at an angle of 30∘ from the horizontal as shown in the figure. The acceleration of the block will be [g=10m/s2]
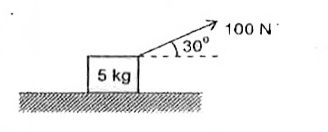 A(10−√3)√3m/s2B20m/s2CzeroD10√3m/s2
A(10−√3)√3m/s2B20m/s2CzeroD10√3m/s2
A block of mass 1kg lies on a horizontal surface in a turck, the coefficient of static fricition between the block and the surface is 0.6, what is the force of fricition on the block. If the acceleration of the truck is 5m/s2.
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
View Solution

