A block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
2.5 N
0.98 N
4.9 N
0.49 N
To solve the problem, we need to determine the magnitude of the frictional force acting on the block held against the wall. Let's break it down step by step.
Step 1: Identify the forces acting on the block
The forces acting on the block are:
- The applied horizontal force (F) = 5 N (to the right)
- The weight of the block (W) = mg (downward)
- The normal force (N) exerted by the wall (perpendicular to the wall)
- The frictional force (f) acting upward (opposing the weight)
Step 2: Calculate the weight of the block
The weight of the block can be calculated using the formula:
W=mg
Where:
- m=0.1kg (mass of the block)
- g=9.8m/s2 (acceleration due to gravity)
Calculating the weight:
W=0.1kg×9.8m/s2=0.98N
Step 3: Determine the normal force
Since the block is in equilibrium, the normal force (N) exerted by the wall is equal to the applied horizontal force (F):
N=F=5N
Step 4: Calculate the maximum frictional force
The maximum frictional force (f_max) can be calculated using the formula:
fmax=μN
Where:
- μ=0.5 (coefficient of friction)
- N=5N
Calculating the maximum frictional force:
fmax=0.5×5N=2.5N
Step 5: Determine the actual frictional force
Since the block is in equilibrium and the weight of the block (0.98 N) is less than the maximum frictional force (2.5 N), the actual frictional force (f) will be equal to the weight of the block:
f=W=0.98N
Conclusion
The magnitude of the frictional force acting on the block is 0.98 N.
---
The forces acting on the block are:
- The applied horizontal force (F) = 5 N (to the right)
- The weight of the block (W) = mg (downward)
- The normal force (N) exerted by the wall (perpendicular to the wall)
- The frictional force (f) acting upward (opposing the weight)
The weight of the block can be calculated using the formula:
W=mg
Where:
- m=0.1kg (mass of the block)
- g=9.8m/s2 (acceleration due to gravity)
W=0.1kg×9.8m/s2=0.98N
Since the block is in equilibrium, the normal force (N) exerted by the wall is equal to the applied horizontal force (F):
N=F=5N
The maximum frictional force (f_max) can be calculated using the formula:
fmax=μN
Where:
- μ=0.5 (coefficient of friction)
- N=5N
fmax=0.5×5N=2.5N
Since the block is in equilibrium and the weight of the block (0.98 N) is less than the maximum frictional force (2.5 N), the actual frictional force (f) will be equal to the weight of the block:
f=W=0.98N
The magnitude of the frictional force acting on the block is 0.98 N.
Topper's Solved these Questions
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:CONSOLIDATED EXERCISE.
Explore 1 Video
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:CONSOLIDATED EXERCISE. (MULTIPAL-CHOICE QUESTION WITH ONE OR MORE THAN ONE CORRECT ANSWER)
Explore 3 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:OLYMPIAD AND NTSE LEVEL EXERCISES (Read the given statements and select the correct option.)
Explore 1 Video
- ELASTICITYBook:CENGAGE PHYSICSChapter:ELASTICITYExercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
- SOUNDBook:CENGAGE PHYSICSChapter:SOUNDExercise:OLYMPIAD AND NTSE LEVEL EXERCISE
Explore 10 Videos
Similar Questions
A block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View Solution
Knowledge Check
A block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
A2.5NB0.98NC4.9ND0.49NA block of mass 6 kg is being pulled by force 24 N as shown . If coefficient of friction between the block and the surface is 0.6 , frictional force acting on the block is :
 A36 NB32 NC12 NDnone of these
A36 NB32 NC12 NDnone of theseIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5N
A block of mass 2 kg is pressed against a rigid vertical wall by a horizontal force of 100 N. If co-efficient of static and kinetic friction are each equal to 0.3 then find the magnitude and direction of frictional force on the block.

View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
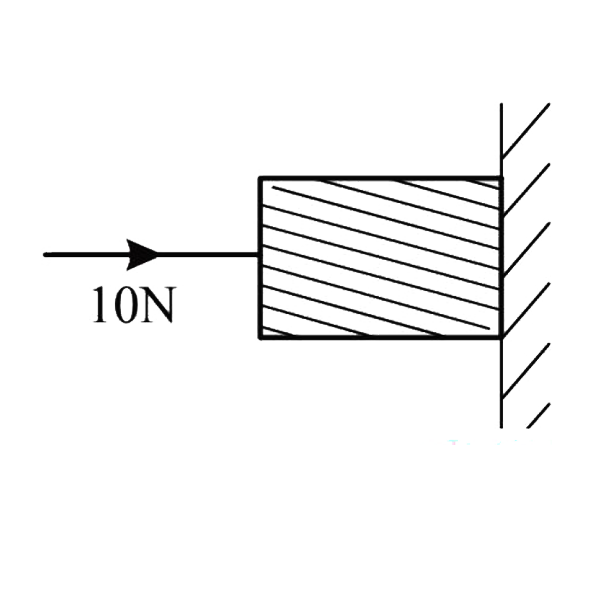
View SolutionA force of 100N is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is 1/4. The friction force acting on the block is :
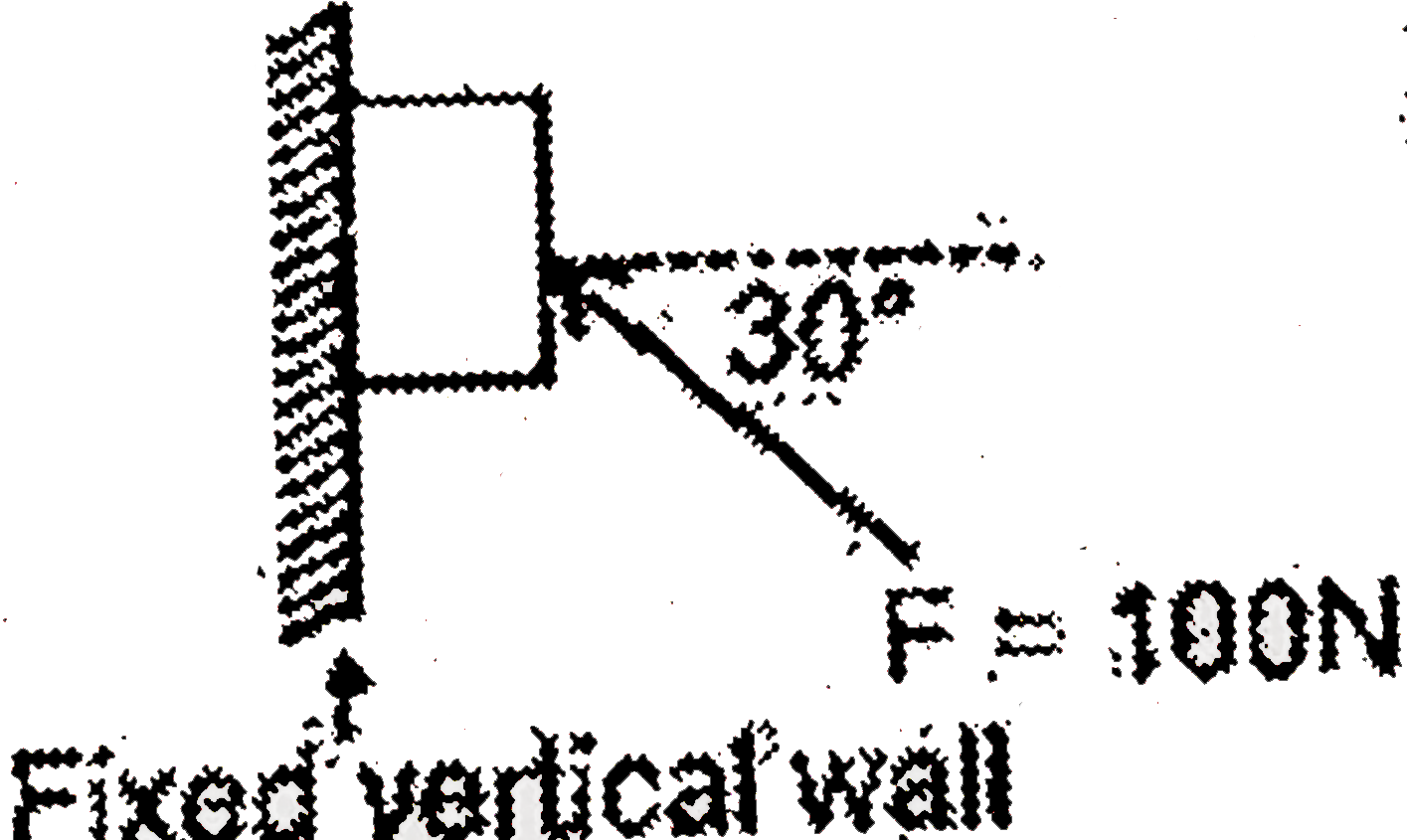
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is

View Solution