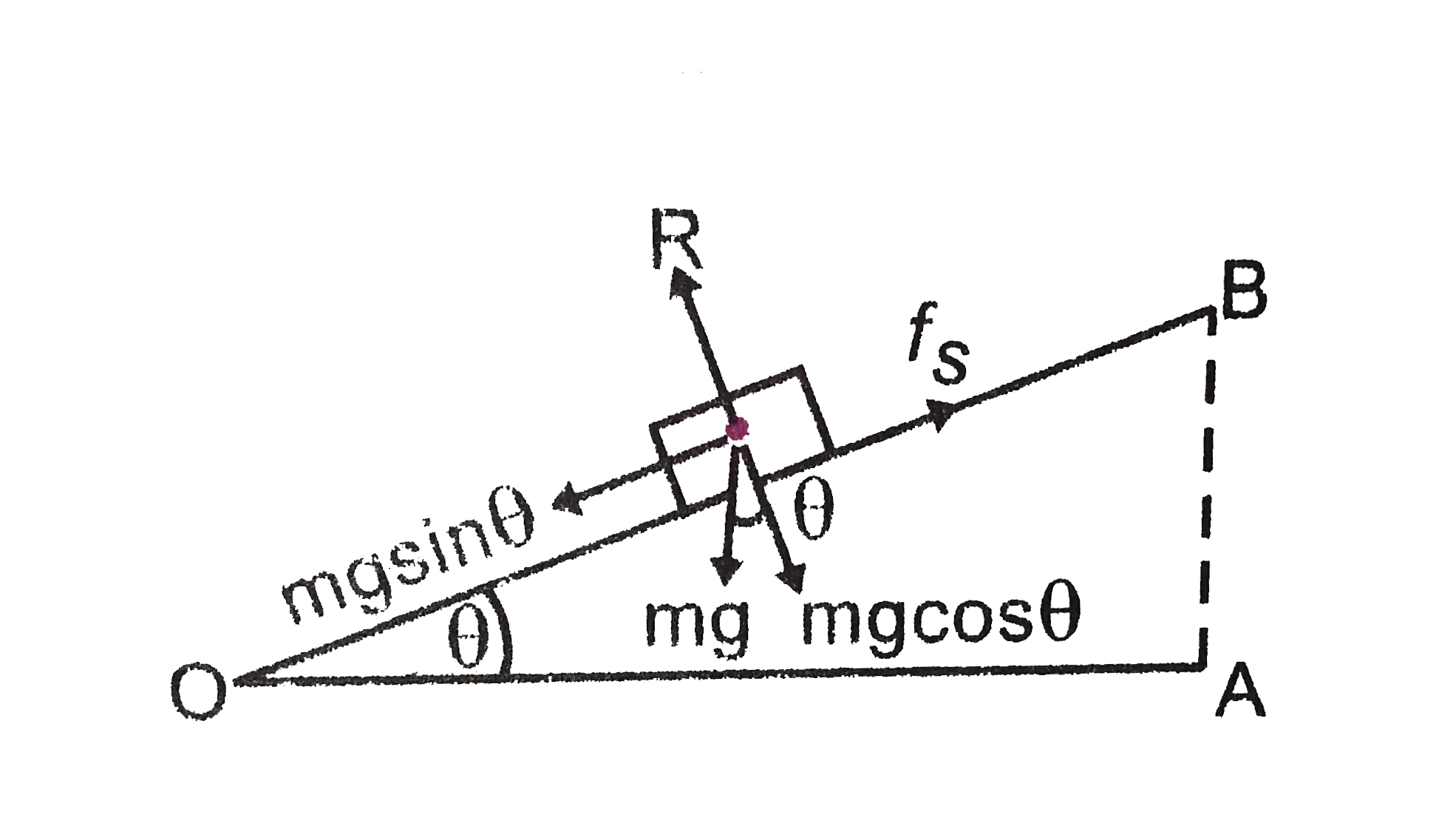
A rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the rocket, making an angle o with the horizontal, a point object of mass m is kept. The maximum coefficient of friction between the mass and the inclined surface such that the mass does not move is

$tan 2 θ$

$tan θ$

$3 tan θ$

$2 tan θ$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the forces acting on the mass on the inclined plane inside the rocket. The rocket is accelerating upwards with an acceleration of $2 g$ , where $g$ is the acceleration due to gravity.
1. Identify the Forces Acting on the Mass:
- The mass $m$ experiences gravitational force downward, which is $m g$ .
- Due to the rocket's upward acceleration of $2 g$ , the effective gravitational force acting on the mass becomes $3 g$ (since $g + 2 g = 3 g$ ).
- The normal force $N$ acts perpendicular to the inclined plane.
2. Components of Forces:
- The gravitational force can be resolved into two components:
- Perpendicular to the inclined plane: $3 m g cos θ$
- Parallel to the inclined plane: $3 m g sin θ$
3. Frictional Force:
- The frictional force $F_{f}$ that prevents the mass from sliding down the incline is given by:
$F_{f} = μ N$
- Where $μ$ is the coefficient of friction and $N$ is the normal force.
4. Normal Force Calculation:
- The normal force $N$ acting on the mass is equal to the perpendicular component of the effective gravitational force:
$N = 3 m g cos θ$
5. Setting Up the Equation:
- For the mass to remain at rest on the incline, the frictional force must be equal to or greater than the component of the gravitational force acting down the incline:
$F_{f} \geq 3 m g sin θ$
- Substituting for $F_{f}$ :
$μ N \geq 3 m g sin θ$
- Substituting for $N$ :
$μ (3 m g cos θ) \geq 3 m g sin θ$
6. Simplifying the Equation:
- Dividing both sides by $3 m g$ (assuming $m \neq 0$ and $g \neq 0$ ):
$μ cos θ \geq sin θ$
7. Finding Maximum Coefficient of Friction:
- Rearranging gives:
$μ \geq \frac{sin θ}{cos θ}$
- This simplifies to:
$μ \geq tan θ$
Final Answer:
The maximum coefficient of friction $μ$ such that the mass does not move is:
$μ = tan θ$

Updated on:8/8/2024