An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
mgsinθ
μmgcosθ
μmgcosθ−mgsinθ
μmgcosθ+mgsinθ
The correct Answer is:D
To solve the problem of finding the minimum force that must be applied to an inclined plane to make a body of mass m move up the plane, we can follow these steps:
1. Identify the Forces Acting on the Body:
- The weight of the body W=mg acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
2. Determine the Normal Force:
- The normal force N acting on the body is equal to the perpendicular component of the weight:
N=mgcosθ
3. Calculate the Frictional Force:
- The frictional force f that opposes the motion of the body up the incline is given by:
f=μN=μ(mgcosθ)
4. Set Up the Equation for Motion:
- For the body to just start moving up the incline, the applied force F must overcome both the gravitational component pulling it down the incline and the frictional force. Therefore, we can write:
F=W∥+f
- Substituting the expressions for W∥ and f:
F=mgsinθ+μ(mgcosθ)
5. Simplify the Expression:
- Factor out mg:
F=mg(sinθ+μcosθ)
Final Result:
The minimum force F that must be applied to the inclined plane to make the body just move up the inclined plane is:
F=mg(sinθ+μcosθ)
- The weight of the body W=mg acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
- The normal force N acting on the body is equal to the perpendicular component of the weight:
N=mgcosθ
- The frictional force f that opposes the motion of the body up the incline is given by:
f=μN=μ(mgcosθ)
- For the body to just start moving up the incline, the applied force F must overcome both the gravitational component pulling it down the incline and the frictional force. Therefore, we can write:
F=W∥+f
- Substituting the expressions for W∥ and f:
F=mgsinθ+μ(mgcosθ)
- Factor out mg:
F=mg(sinθ+μcosθ)
The minimum force F that must be applied to the inclined plane to make the body just move up the inclined plane is:
F=mg(sinθ+μcosθ)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 3 Section-A
Explore 22 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 3 Section-B
Explore 12 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 2 SECTION-E:- Static friction, Kinetic friction
Explore 13 Videos
- MODERN PHYSICS -1Book:MOTIONChapter:MODERN PHYSICS -1Exercise:EXERCISE-4 ( LEVEL- II)
Explore 39 Videos
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCISE-4 ( LEVEL-II)
Explore 15 Videos
Similar Questions
A block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ . The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down . If we define N=10μ , then N is :
View Solution
Knowledge Check
A smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
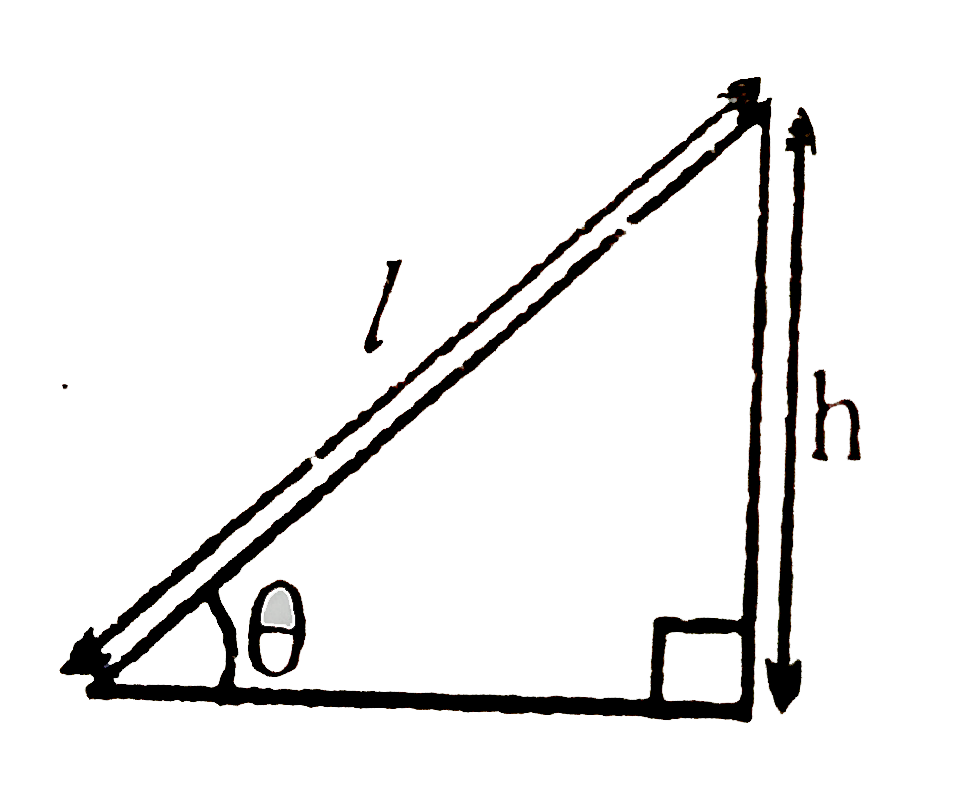 A√2hgB√2lgC√2lgsinθD1sinθ√h2g
A√2hgB√2lgC√2lgsinθD1sinθ√h2gIn the above problem, the minimum force required to pull the body up the inclined plane
A66.6 NB86.6 NC96.6 ND76.6 NA body of mass 10 kg is lying on a rough plane inclined at an angle of 30∘ to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane is
A914 NB91.4 NC9.14 ND0.914 N
A block moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ the force required to just push it up the inclined plane is three times the force required to just prevent it from sliding down. If we define N=10μN then N is
View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define N=10μ, then N is
View SolutionA cubical block rests on an inclined plane of coefficient of friction μ=1√3 . What should be the angle of inclination so that the block just slides down the inclined plane?
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View Solution