A hollow smooth uniform $A$ of mass 'm' rolls without sliding on a smooth horizontal surface collides head to elastically with another stationary smooth solid sphere $B$ of the same mass $m$ and same radius. The ratio of kinetic energy of 'B' to that of 'A' just after the collision is -
.

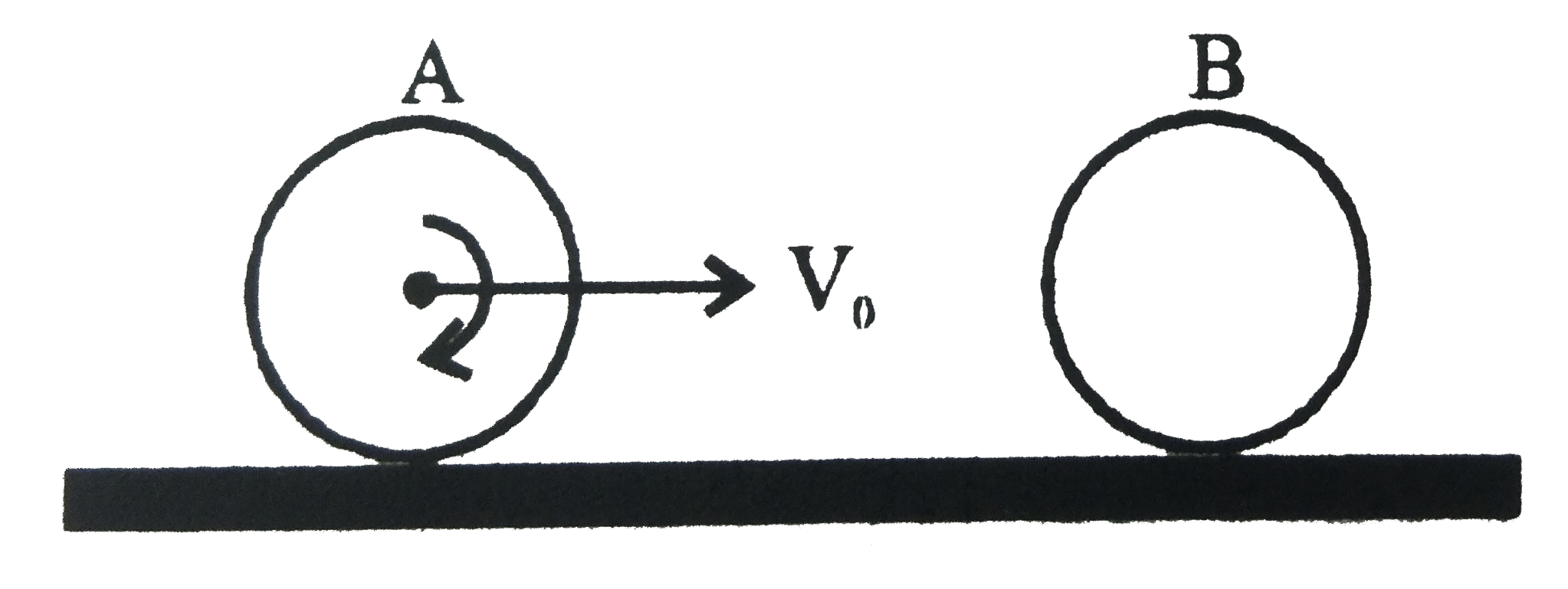$1 : 1$

$2 : 3$

$3 : 2$

None

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A uniform solid sphere A of mass m is rolling without sliding on a a smooth horizontal surface. It collides elastically and head - on with another stationary hollow sphere B of the same mass and radius. Assuming friction to be absent everywhere, the ratio of the kinetic energy of B to that of A just after the collision is

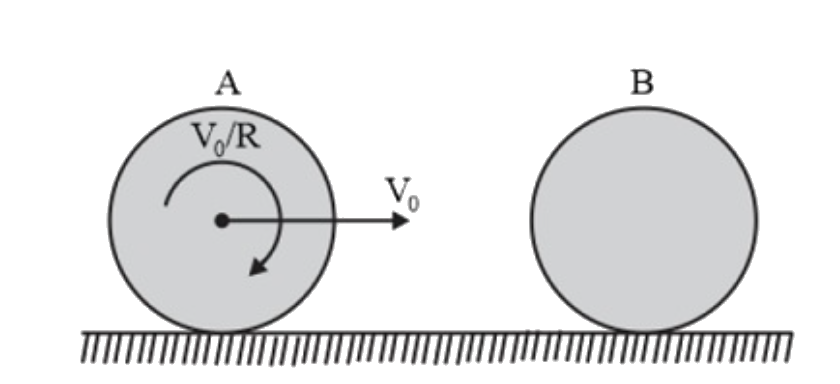A $5 : 2$
B $1 : 1$
C $2 : 3$
D $3 : 2$
A solid sphere of mass $m$ and radius $R$ rolls without slipping on a horizontal surface such that $v_{c . m .} = v_{0}$ .
AThe kinetic energy of rotation is $\frac{1}{5} m v_{0}^{2}$ .
BThe total kinetic energy is $\frac{7}{10} m v_{0}^{2}$ .
CThe mechanical energy (assume the ground as reference) is $m g R + \frac{7}{10} m v_{0}^{2}$ .
DAll options are correct.
A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A $1 / 2 M v^{2}$
B $3 / 2 M v^{2}$
C $M v^{2}$
D $1 / 2 M R^{2} ω^{2}$