A sphere of radius R and mass M collides elastically with a cubical block of mass M and side 2R. The entire system is on a smooth horizontal ground. Given that the sphere was rolling without slipping with an angular velocity ω at the time of collision. The velocities of the sphere and the block after the collision are
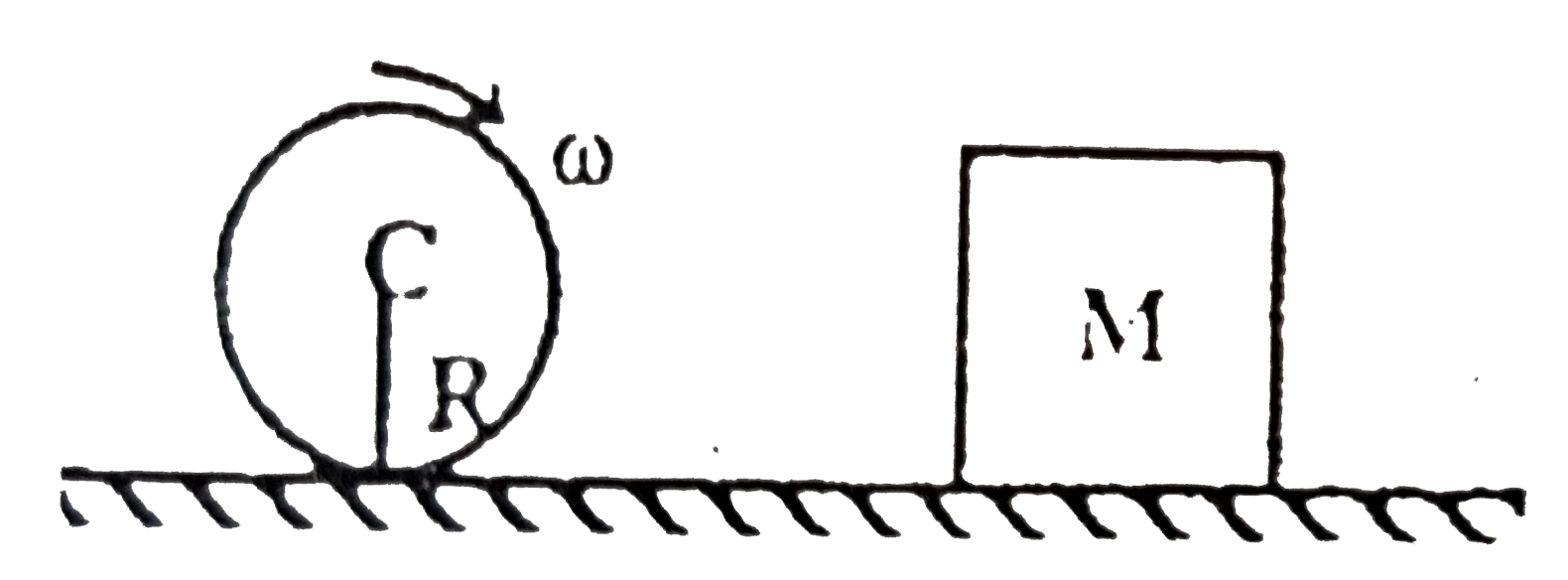
ωsphere=0, vsphere=0, vblock=v
ωsphere=ω, vsphere=0, vblock=v
ωsphere=0, vsphere=0, vblock=0
ωsphere=ω2, vsphere=v2, vblock=v2
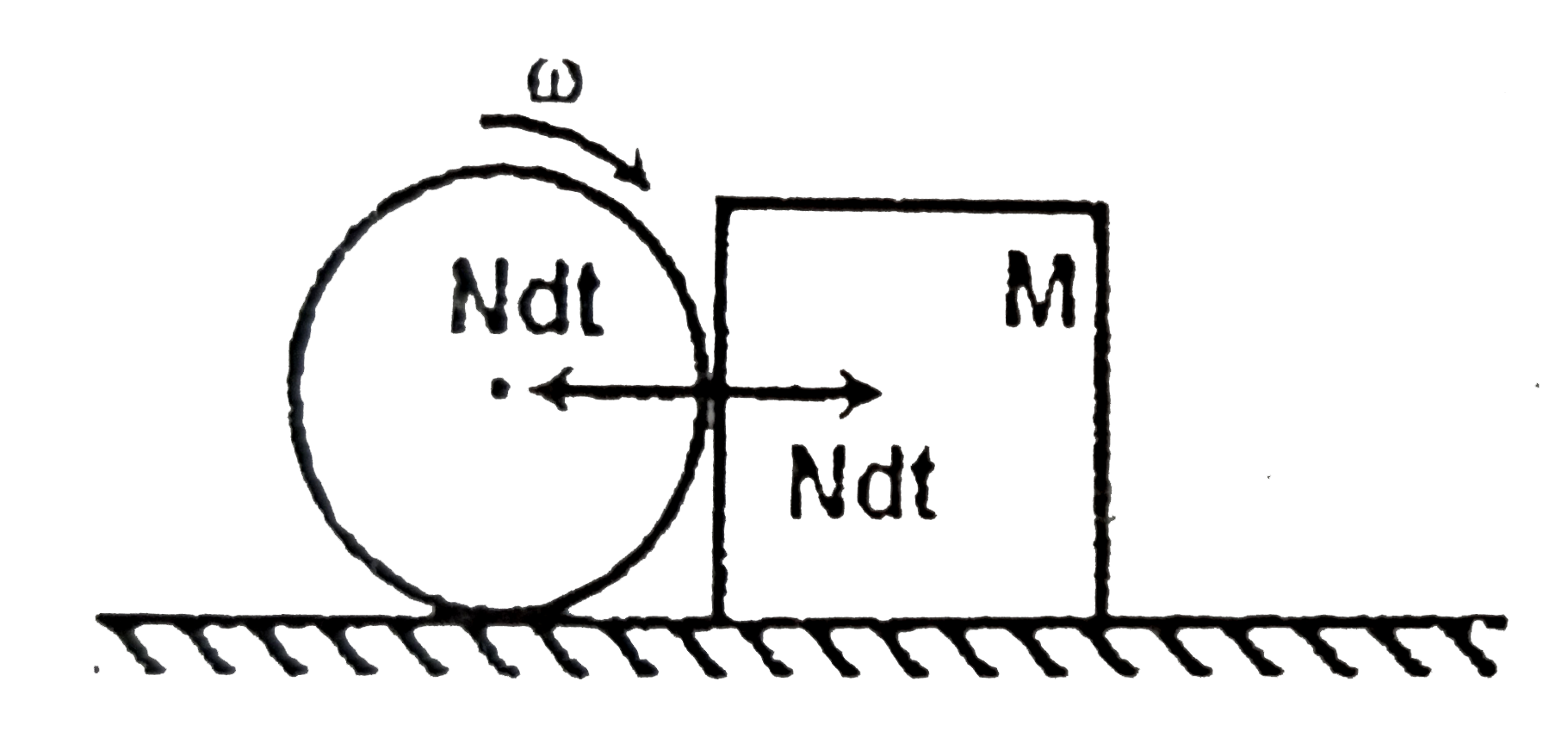
When the sphere collides with the block due to elastic collision, the translational kinetic energy of the sphere gas totally transferred to the block, but rotational kinetic energy of the sphere does not change.
Hence, ωsphere=ω, vsphere=0, vblock=v
Topper's Solved these Questions
Similar Questions
A sphere of mass 8m collides elastically (in one dimension) with a block of mass 2m. If the initial energy of sphere is E. What is the final energy of sphere?
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View Solution
Knowledge Check
If a solid sphere of mass 500 gram rolls without slipping with a velocity of 20 cm/s, then the rolling kinetic energy of the sphere will be
A140 JB280 JC0.014 JD0.028 JA solid sphere of mass 500 gm and radius 10 cm rolls without slipping with the velocity 20cm/s. The total kinetic energy of the sphere will be
A0.028 JB280 JC140 JD0.014 JA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A solid sphere spinning about a horizontal axis with an angular velocity ω is placed on a horizontal surface. Subsequently it rolls without slipping with an angular velocity of :
View SolutionA solid sphere of mass M is placed on the top of a plank of the same mass, after giving an angular velocity ω0 at t=0. Find the velocity of the plank and the sphere when the sphere starts rolling:,

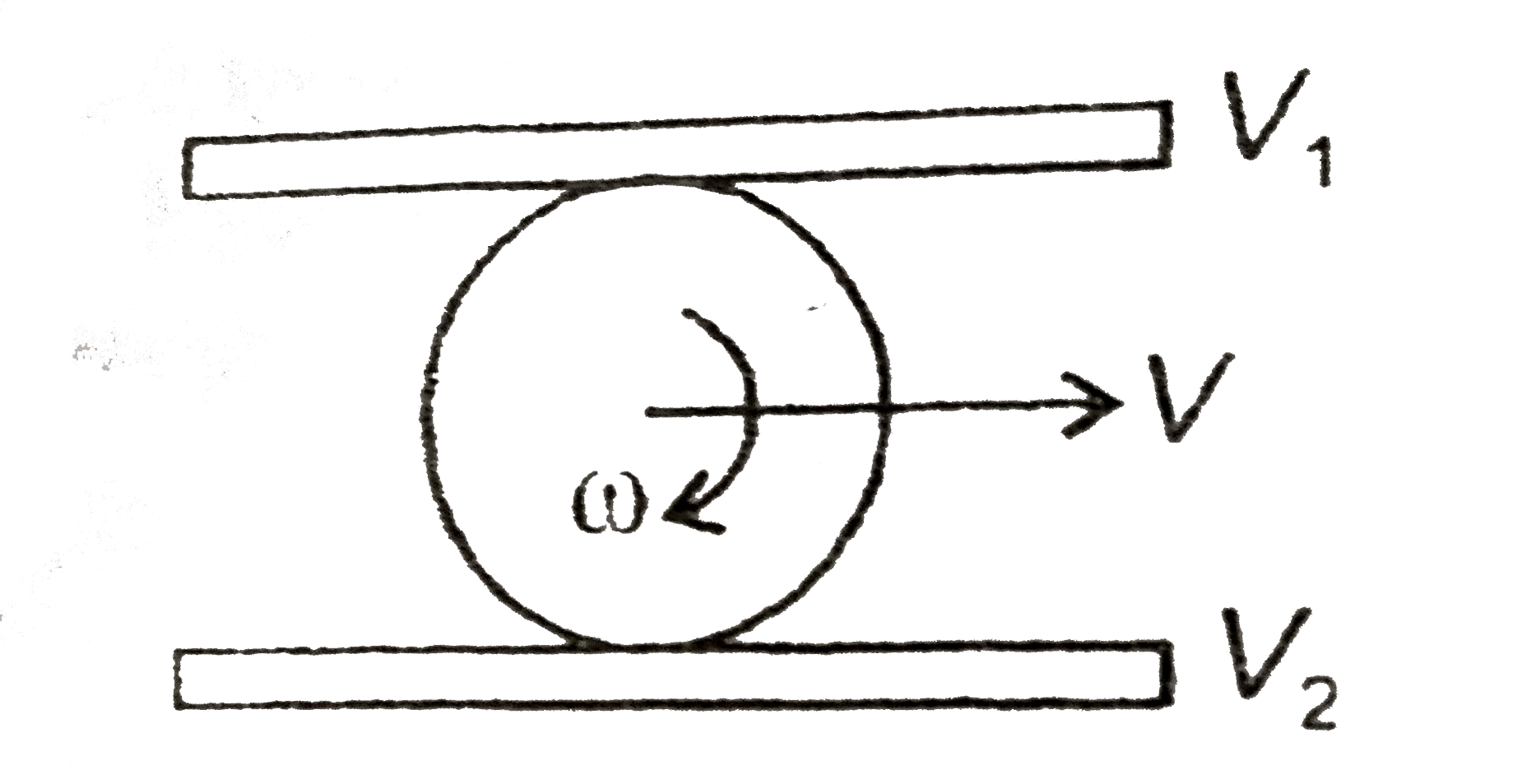
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA block of mas m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of te blocks after the collision.
View SolutionA sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
View Solution

