A cube of side $a$ and mass $M$ is pivoted on a horizontal axis such that it can rotate about one of tis edges. Initially it is held in the highest position and then released. Find horizontal and vertical components of reaction of pivot on the cube at the moment when the reaction toward the centre of the cube becomes zero. Given that $M . I$ of the cube about its edge is equal to $\frac{2}{3} M a^{2}$ .

Video Solution

Text Solution

Verified by Experts

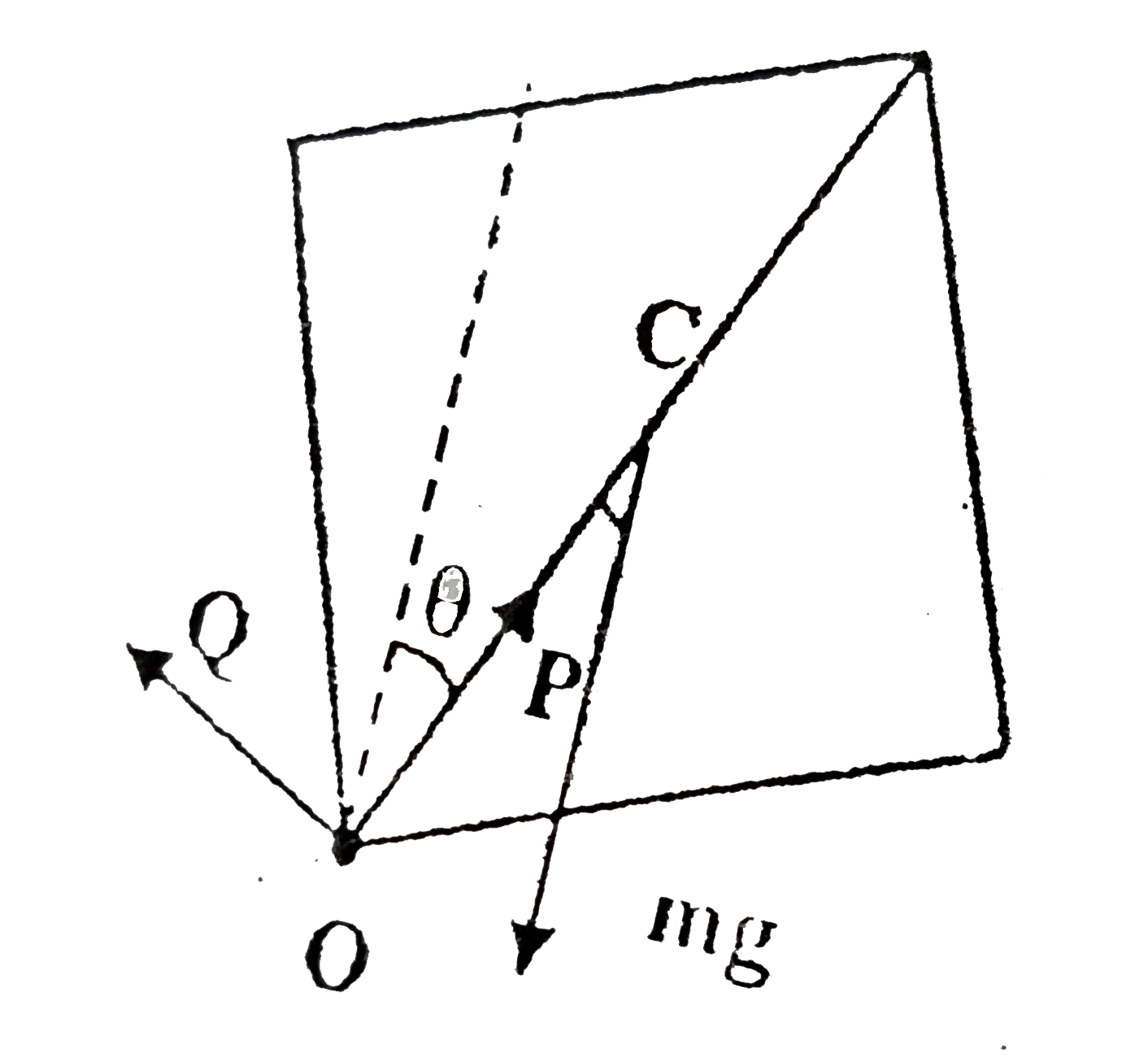
Let $P$ and $Q$ be the components of reaction of pivot on the cube along and perpendicular to the $O C$ .
$M . I .$ of the cube about $O$ is $\frac{2}{3} M a^{2}$
$α = \frac{τ}{I} = M g sin θ . \frac{a}{\sqrt{2}} / \frac{2}{3} M a^{2} = \frac{3}{2 \sqrt{2}} \frac{g sin θ}{a}$ Now along $O C$ , $M g cos θ - P = M \frac{a}{\sqrt{2}} ω^{2}$
Perpendicular to $O C$ , $M g sin θ - Q = M \frac{a}{\sqrt{2}} α$
$Q = (M g sin θ) / 4$
Intergrating $α$ , we get $ω^{2} = \frac{3 g (1 - cos θ)}{a \sqrt{2}}$ .......( $1$ )
$P = M g cos θ - M a \frac{3 g (1 - cos θ)}{2 a} = \frac{- 3}{2} M g + \frac{5}{2} M g cos θ$
When $P = 0$ $cos θ = 3 / 5$ , $sin θ = 4 / 5$
Now horizontal component of reaction is $P sin θ - Q cos θ = (- 3 / 25) M g$
Vertical component of reaction is $P cos θ + Q sin θ = (4 / 25) M g$

Updated on:21/07/2023

A solid cube of side l is made to oscillate about a horizontal axis passing through one of its edges. Its time period will be
A $2 π \sqrt{\frac{2 \sqrt{2}}{3} \frac{l}{g}}$
B $2 π \sqrt{\frac{2}{3} \frac{l}{g}}$
C $2 π \sqrt{\frac{\sqrt{3}}{2} \frac{l}{g}}$
D $2 π \sqrt{\frac{2}{\sqrt{3}} \frac{l}{g}}$
The moment of inertia of a cube of mass m and side a about one of its edges is equal to
A $\frac{2}{3} m a^{2}$
B $\frac{4}{3} m a^{2}$
C $3 m a^{2}$
D $\frac{8}{3} m a^{2}$
If the edge of a cube be 7 cm, then the volume of the cube is:
AA)321 ${cm}^{3}$
BB)343 ${cm}^{3}$
CC)433 ${cm}^{3}$
DD)243 ${cm}^{3}$