A sphere of radius R is projected with a reverse spin ω0 down a rough inclined plane with a speed v0 for which coefficient of friction is μ>tanθ, where θ is angle of the inclination. Show that it will turn back if
ω>5v0μ2R(μ−tanθ)

∵μ>tanθ
⇒μmgcosθ≥mgcosθtanθ
⇒f≥mgsinθ
Hence, the sphere will turn back if at the moment its centre of mass comes to stop it must have angular speed in same direction as ω0 has.
Let at time t, vc.m.=0
⇒v0+(gsinθ−μgcosθ)t=0
⇒t=v0g(μcosθ−sinθ).....(1)
further , ω0−μmgcosθIc.m.t>0.....(2)
From Eq. (1) and (2), we get ω>5v0μ2R(μ−tanθ)
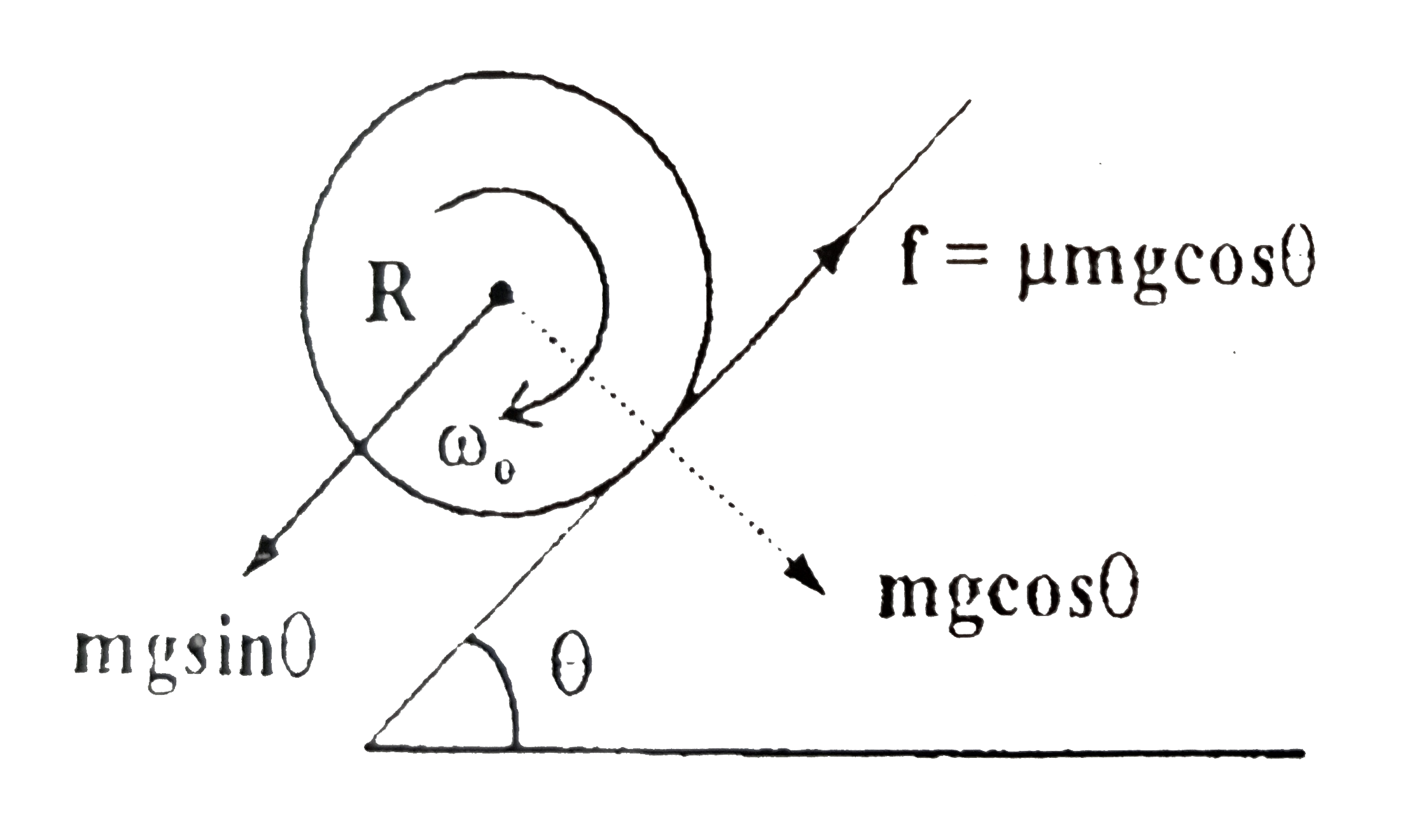
Topper's Solved these Questions
Similar Questions
Show that a cylinder will slip on an inclined plane if the coefficient of static friction between the plane and the cylinder is less than 13tanθ where θ is the angle of the inclination with the horizontal.
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View Solution
Knowledge Check
A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseA body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
Ag2√2Bg2C3g2√2Dg√2A cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time
 AωoR/gsinθB2ω)(o)R/3gsinθC2ωoR/5sinθDωoR/2gsinθ
AωoR/gsinθB2ω)(o)R/3gsinθC2ωoR/5sinθDωoR/2gsinθ
A small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
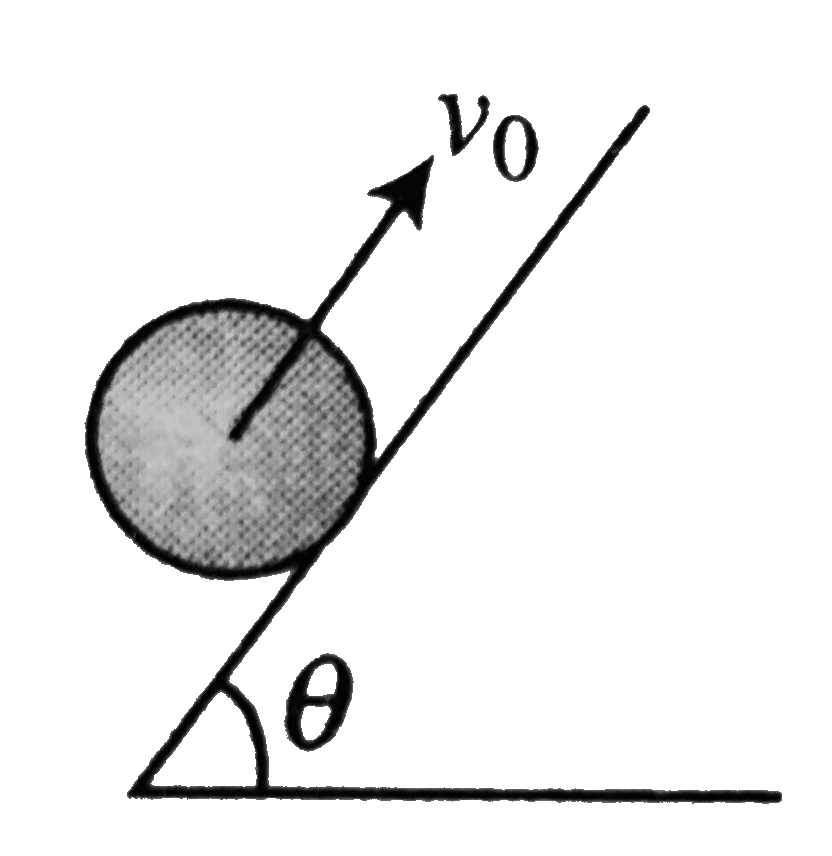
View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
View SolutionA particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
View SolutionA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
View SolutionA ring of mass M and radius R is released on an inclined as shown. If the coefficient of friction μ<12tanθ, then during a displacement l:
View Solution

