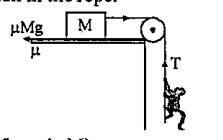
A monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration g/4. The opposite end of the rope is tied to a block of mass M lying on a rough horizontal plane. The coefficient of friction between the block and horizontal plane is μ. Find the tension in the rope.

amonkey/rope=g/4
Let acceleration of M=a0
So, acceleration of rope =a0
→amonkey=→amonkey/rope+→arope=(a0−g/4)
Now for mass M, T−μMg=Ma0……(1)
For monkey mg−T=m(a0−g/4)......(2)
From equation (1) and (2)
mg−μMg=a0(M+m)−mg4
⇒a0=(5m4−μM)g/(M+m)=(5m−4μM)g4(M+m)
∴T=M(5m−4μM)g4(M+m)+μMg

Topper's Solved these Questions
Similar Questions
A monkey of mass 'm' climbs up to a rope hung over a fixed pulley with an acceleration relative to the rope g/4. The opposite end of the rope is tied to a bock of mass M lying on a rough horizontal plane. The coeffient of friction between the block and horizontal plane is μ. Find the tension in the rope
View SolutionA monkey of mass m climbs up to a rope hung over a fixed pulley. The opposite end of the rope is tied to a weight of mass M lying on a horizontal plane. Neglecting the friction, find the acceleration of both the bodies (relative to the plane) and the tension of the rope for the three cases:
(i) The monkey does not move with respect to the rope
(ii) The monkey moves upwards with respect to the rope with acceleration a.
(iii) The monkey moves downwards with respect to the rope, with acceleration a.
View Solution
Knowledge Check
A block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreasesA cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope where the cat move upwards with in acceleration a=2m/s2 relative to the rope ?
 A2 NB12NC8ND4N
A2 NB12NC8ND4NA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The tension of rope isAMm(μg+g+b)M+mBMm(μg−g+b)M+mCMm(μg+g−b)M+mDMm(μg−g−b)M+m
A monkey of massm clings to a rope slung over a fixed pulley. The opposite end of the rope is tied to a weight of
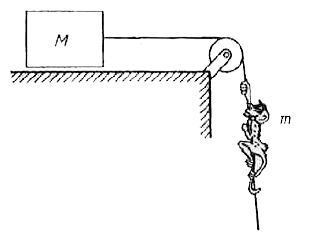
mass M lying on a horizontal plat (Fig.). Neglecting friction find the acceleration of both bodies (relative to the plate) and the tension of the rope for the three cases:
(1) the monkey does not move with respect to the rope,
(2) the monkey moves upwards with respect to the rope with acceleration b,
(3) the monkey moves downwards with respect to the rope with an acceleration b.
View SolutionA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View Solution

