Shown in the diagram is a system of two bodies, a block of mas m and a disc of mass M, held in equilibrium. If the string 3 is burnt, find the acceleration of the disc. Neglect the masses of the pulleys P and Q. (The coefficient of friction between the block and horizontal surface is μ)

Referring to the free-body diagram we write the equation of motion.
For the block m :
T1−μN=ma1……(1)
and N−mg=0…(2)
For pulley P :
mpg+T2−2T1=mpap
Since the pulley is light,
∴mp≈0
⇒T2=2T1.....(3)
For disc M.
Mg−2T2=Ma2......(4)
From the geometry of the figure the positions of the parts m, P and M are related as x1+2y1=l1 and (y2−y1)+y2=l2, where l1 and l2 are the lengths of the strings 1 and 2, respectively. Eliminating y1 from these two equations, we obtain,
x1+4y2=l1+2l2 ,
Differntiating both sides twice w.r.t. time, we obtain d2x1dt2+4d1y2dt2=0
⇒a1=4a2.....(5)
From Eqs. (1) and (2), we get
T1−μmg=ma1.......(6)
From Eqs. (3) and (4), we get
Mg−4T1=Ma2.....(7)
Eliminating T1 from Eqs. (6) and (7) and putting a1=4a2, we obtain
a2=M−4μmM+16mg.

Topper's Solved these Questions
Similar Questions
In the arrangement shown in fig neglect the masses of pulleys and string and also friction Calculate acceleration of blocks A and B

View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
Knowledge Check
A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of theseIn the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is
 AMg directed upBμ mg directed upC(M-m) g directed downDμ mg directed down
AMg directed upBμ mg directed upC(M-m) g directed downDμ mg directed downA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreases
A block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
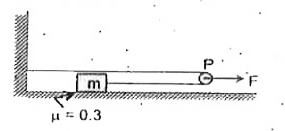
View SolutionIn terms of masses m1,m2 and g, find the acceleration of both the blocks shown in Fig. Neglect all friction and masses of the pulley.
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View Solution

