Find the minimum force required to keep a block of mass $m$ in equilibrium on a rough inclined plane with inclination $α$ and coefficient of friction $μ (< tan α)$ .

Video Solution

Text Solution

Verified by Experts

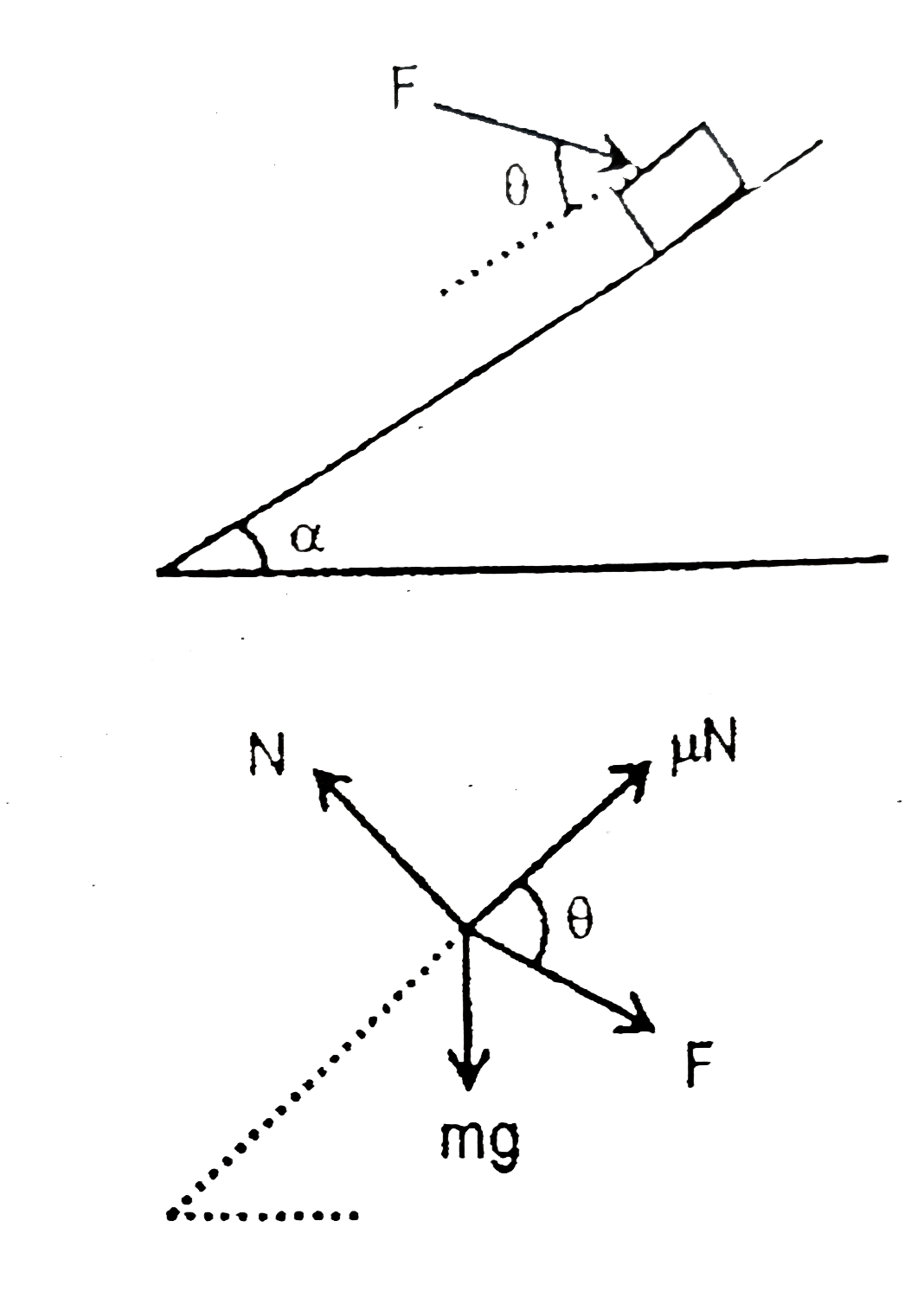
In order to achieve a minimum of $F$ , it should be directed as shown in the figure. The value of $θ$ can be found using the $F B D$ of the block.
Normal to the incline,
$N = m g cos α + F sin θ$ …..( $i$ )
Along the incline
$μ N + F cos θ = m g sin α$ ....( $i i$ )
From ( $i$ ) and ( $i i$ ) , we get
$F = \frac{m g (sin α - μ cos α)}{cos θ + μ sin θ}$
For $F$ to be minimum
$\frac{d}{d θ} (cos θ + μ sin θ) = 0$
$\Rightarrow μ = tan θ$
$F_{min} = \frac{m g (sin α - μ cos α) \sqrt{1 + μ^{2}}}{1 + μ}$

Updated on:21/07/2023

A block of mass m in the equilib rium on a rough inclined plane with inclination $α$ and coefficient of friction as shown in the figure $(μ < tan α)$ . A force F is applied on the block which makes an angle $θ$ with the horizontal as shown in diagram.

ANormal force on the block $m g cos α + F sin θ$ .
BMinimum force f to keep the blockin equilibrium $F_{min} = \frac{m g (sin α - μ cos α)}{2 μ} \sqrt{1 + μ^{2}}$
C $μ = tan θ$
DNone of these
A body of mass m slides down a rough plane of inclination $α$ . If $μ$ is the coefficient of friction, then acceleration of the body will be
A $g sin α$
B $μ cos α$
C $g (sin α - μ cos α)$
D $g (cos α - μ sin α)$
A block of mass m is at rest on a rough inclined plane, whose friction coefficient is $μ .$ Net force exerted by surface on block is :-
Amg
Bmg sin $θ$
C $μ m g cos θ$
D $μ m g sin θ$