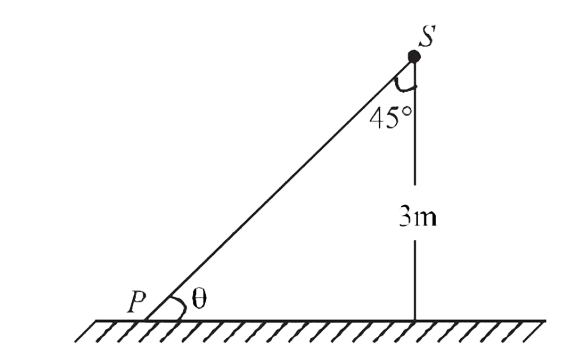
A spot light S rotates in a horizontal plane with a constant angular velocity of 0.1rad/s. The spot of light P move along the wall at a disatnce 3m. What is the velocity of the spot P when θ=45∘ ?
To solve the problem, we need to find the velocity of the spot of light P on the wall when the angle θ is 45∘. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Geometry
We have a spotlight S rotating with a constant angular velocity ω=0.1rad/s at a distance OQ=3m from the wall. The angle θ is the angle between the line from the spotlight to the wall and the vertical line from the wall to the spotlight.
Step 2: Relate the Angle to the Distance
Using the tangent function in the right triangle OQP:
tan(θ)=QPOQ
Where QP is the horizontal distance from the point directly below the spotlight to the point P on the wall.
Step 3: Express QP in Terms of θ
From the above equation, we can express QP:
QP=OQ⋅tan(θ)=3⋅tan(θ)
Step 4: Differentiate with Respect to Time
To find the velocity of point P, we differentiate QP with respect to time t:
d(QP)dt=3d(tan(θ))dt
Using the chain rule:
d(tan(θ))dt=sec2(θ)⋅dθdt
Step 5: Substitute the Angular Velocity
Since dθdt=ω=0.1rad/s:
d(QP)dt=3⋅sec2(θ)⋅ω
Step 6: Calculate sec2(45∘)
At θ=45∘:
sec2(45∘)=2
Step 7: Substitute Values
Now substituting sec2(45∘) and ω:
d(QP)dt=3⋅2⋅0.1=0.6m/s
Final Answer
Thus, the velocity of the spot P when θ=45∘ is:
Velocity of P=0.6m/s
---
We have a spotlight S rotating with a constant angular velocity ω=0.1rad/s at a distance OQ=3m from the wall. The angle θ is the angle between the line from the spotlight to the wall and the vertical line from the wall to the spotlight.
Using the tangent function in the right triangle OQP:
tan(θ)=QPOQ
Where QP is the horizontal distance from the point directly below the spotlight to the point P on the wall.
From the above equation, we can express QP:
QP=OQ⋅tan(θ)=3⋅tan(θ)
To find the velocity of point P, we differentiate QP with respect to time t:
d(QP)dt=3d(tan(θ))dt
d(tan(θ))dt=sec2(θ)⋅dθdt
Since dθdt=ω=0.1rad/s:
d(QP)dt=3⋅sec2(θ)⋅ω
At θ=45∘:
sec2(45∘)=2
Now substituting sec2(45∘) and ω:
d(QP)dt=3⋅2⋅0.1=0.6m/s
Thus, the velocity of the spot P when θ=45∘ is:
Velocity of P=0.6m/s
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:VALUE BASED QUESTIONS
Explore 5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:CURIOSITY QUESTIONS
Explore 4 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A spotlight S rotates in a horizontal plane with a constant angular velocity of 0.1rads. The spot P of light moves along the wall at a distance 3m. The velocity of the spot P when θ=45∘ is v(mathrm~ms). Find 5v.
'(##CEN_KSR_PHY_JEE_C07_029_Q18##)'
View SolutionSpotlight S rotates in a horizontal plane with constant angular velocity of 0.1 radian //second.Thespotoflightpmovesalongthewallatadistanceof3 m .Thevelocityofthespotpwhentheta = 45(@)(see−fig.)is……….. m//s
View Solution
Knowledge Check
A wheel rotates with a constant angular velocity of 600 rpm. What is the angle through which the wheel rotates in 1s?
A5π radB20πradC15π radD10π radA plane mirror rotating at an angular velocity of 3 radian/s reflects a light beam. The angular velocity of the reflected beam is -
A3rad/sB6rad/sC9rad/sD12rad/sA body of mass 10 kg is moving in a circle of radian 1 m with an angular velocity of 2rad/s the centripetal force is
A10 NB40 NC30 ND20 N
A wheel starting from rest via rotating with a constant angular velocity of 3 rad s−1. What is its angular acceleration after 4 s?
View SolutionA closed chain A of mass m = 0.36kg is attached to a vertical rotating shaft by means of thread showin in fig. and rotated with a constant angular velocity ω=35rad/s. The thread forms an angle θ=45∘ with the vertical. Then the tension of the thread is
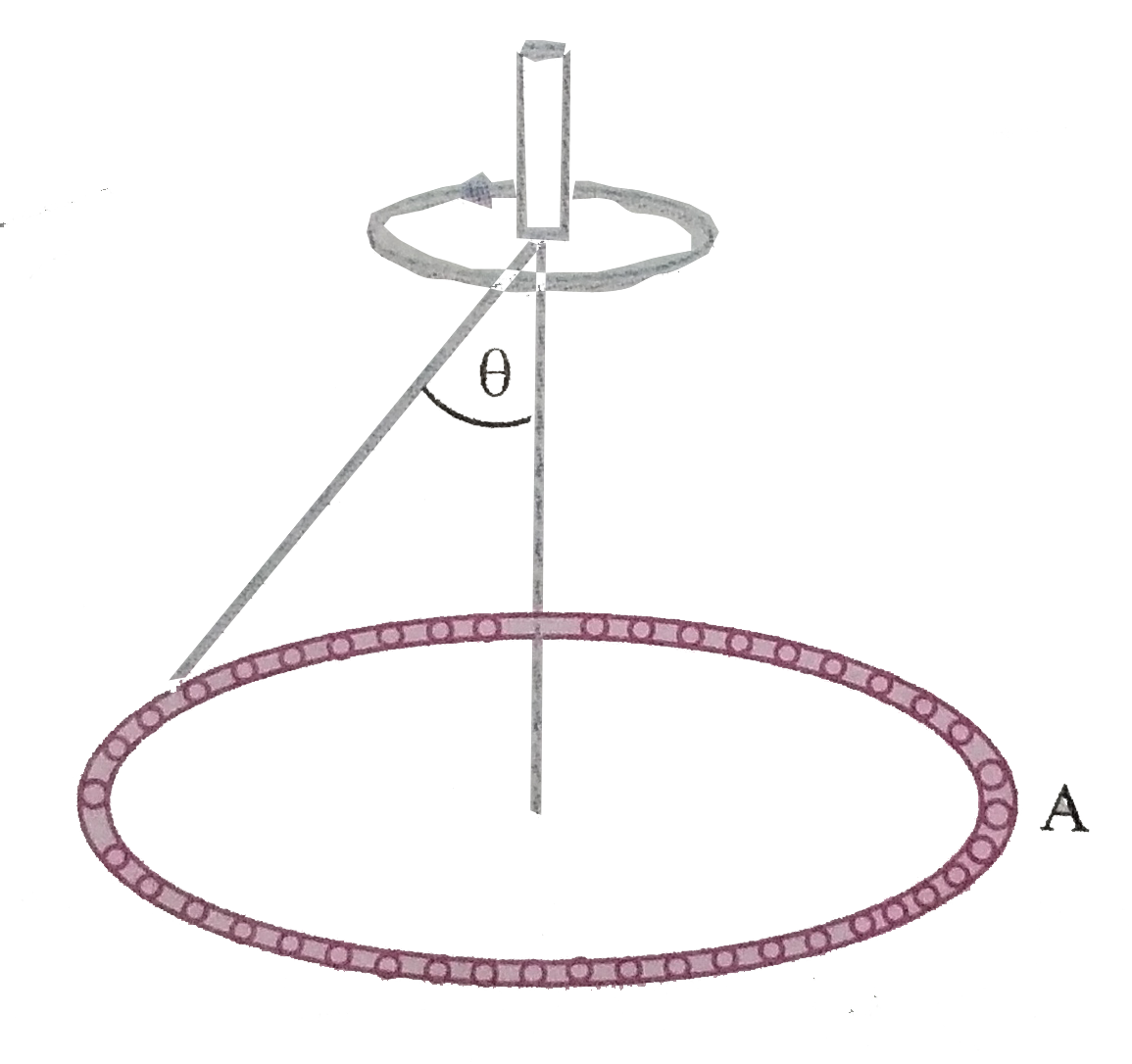
View SolutionA closed chian A of mass m=0.36kg is attached to a vertical rotating shaft by means of a thread (figuer), and rotates with a constant angular velocity ω=35rad/s. The thread forms an angle θ=45∘ with the vertical. Find the distance between the chain's of the thread.

View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionTwo disks are rotating about the same axis. Disk A has a moment of inertia of 3.4kg−m2 and an angular velocity of +72rad/s. Disk B is rotating with an angular velocity of −9.8rad/s. The two disks are then linked together without the aid of any external torques, so that they rotate as a single unit with an angular velocity of −2.4rad/s. The axis of rotation for this unit is the same as that for the separate disks. What is the moment of inertia of disk B?
View Solution

