Point masses $m_{1} and m_{2}$ are placed at the opposite ends of a rigid rod of length $L$ , and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point $P$ on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity $ω_{0}$ is minimum, is given by :

Video Solution

Text Solution

Verified by Experts

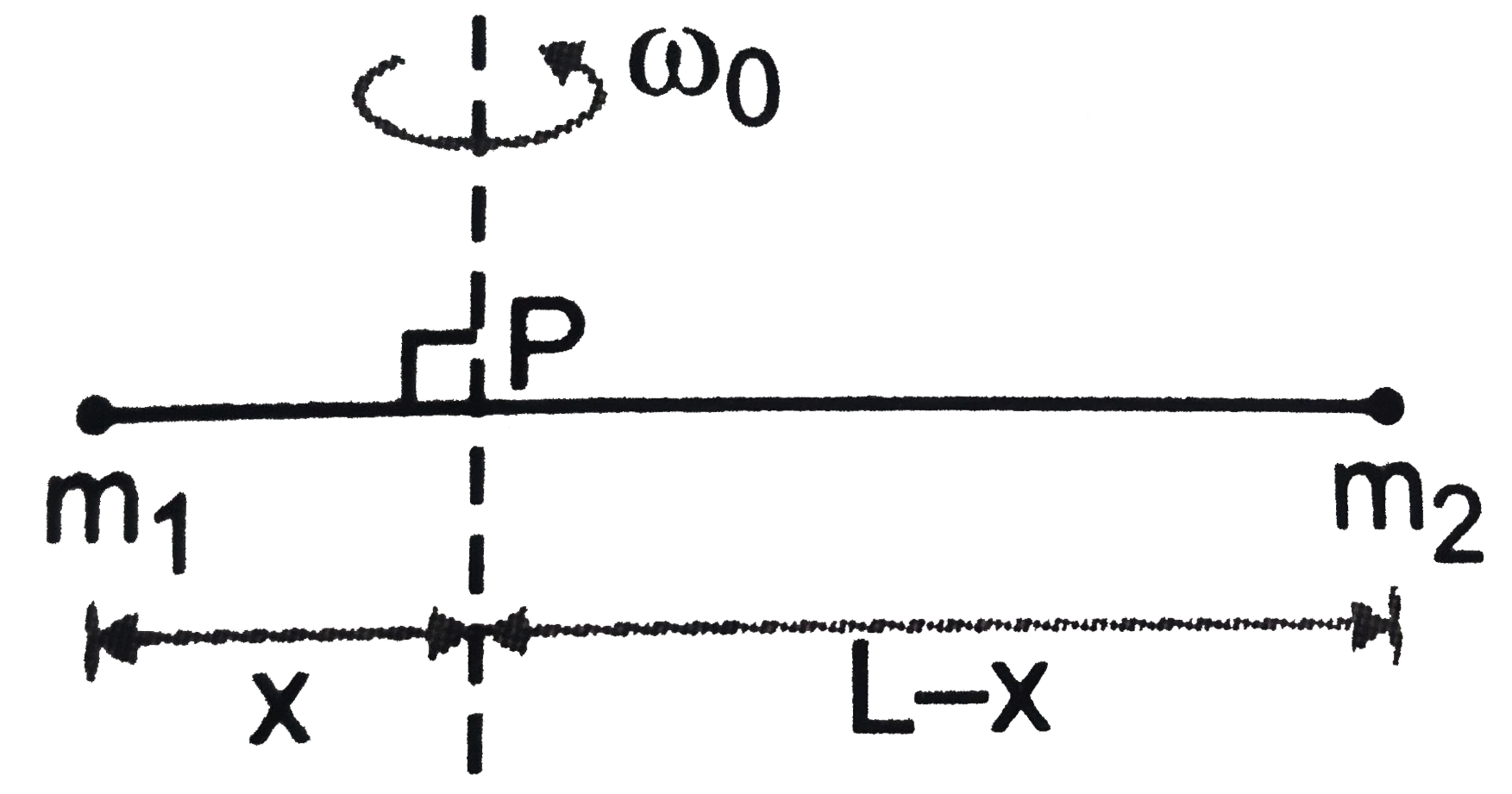
Let the axis of rotation be at a distance x from $m_{1}$ Fig $K . E .$ of translation $= 0$
$K . E .$ of rotation $= \frac{1}{2} (I_{1} + I_{2}) ω_{0}^{2}$
According to work energy principle,
Work done = Increase in energy
$W = \frac{1}{2} (I_{1} + I_{2}) ω_{0}^{2} = \frac{1}{2} [m_{1} x^{2} + m_{2} {(L - x)}^{2}] ω {(0)}^{2}$ ..(i)
For $W$ to be minimum, $\frac{d W}{d x} = 0$
From (i), $\frac{d W}{d x} = \frac{1}{2} m_{1} 2 x + \frac{1}{2} m_{2} \times 2 (L - x) = 0 or m_{1} x - m_{2} (L - x) = 0 or (m_{1} + m_{2}) x = m_{2} L$
$x = m_{2} L / (m_{1} + m_{2})$
This is the position of centre of mass of the ord from $m_{1}$ . Hence the required axis should pass through centre of mass of the rod and perpendicular to the length of the rod as shown in Fig.

Updated on:21/07/2023

Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
A0,42 m from mass of 0.3 kg
B0.70 m form mass of 0.7 kg
C0.98 m form mass of 0.3 kg
D0.98 m from mass of 0.7 kg
Two point masses of 0.3 kg and 0.7 kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
A0.42 in from mass of 0.3 kg
B0.70 m from mass of 0.7 kg
C0.98 m from mass of 0.3 kg
D0.98 m from mass of 0.7 kg.
A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

A $\frac{g}{2 l ω^{2}}$
B $\frac{g}{l ω^{2}}$
C $\frac{2 g}{{(l ω)}^{2}}$
D $\frac{3 g}{2 l ω^{2}}$