Show that →a.(→b×→c) is equal in magnitude to the volume of the parallelopiped formed on the three vectiors, →a,→band→c.
Video Solution
Text Solution
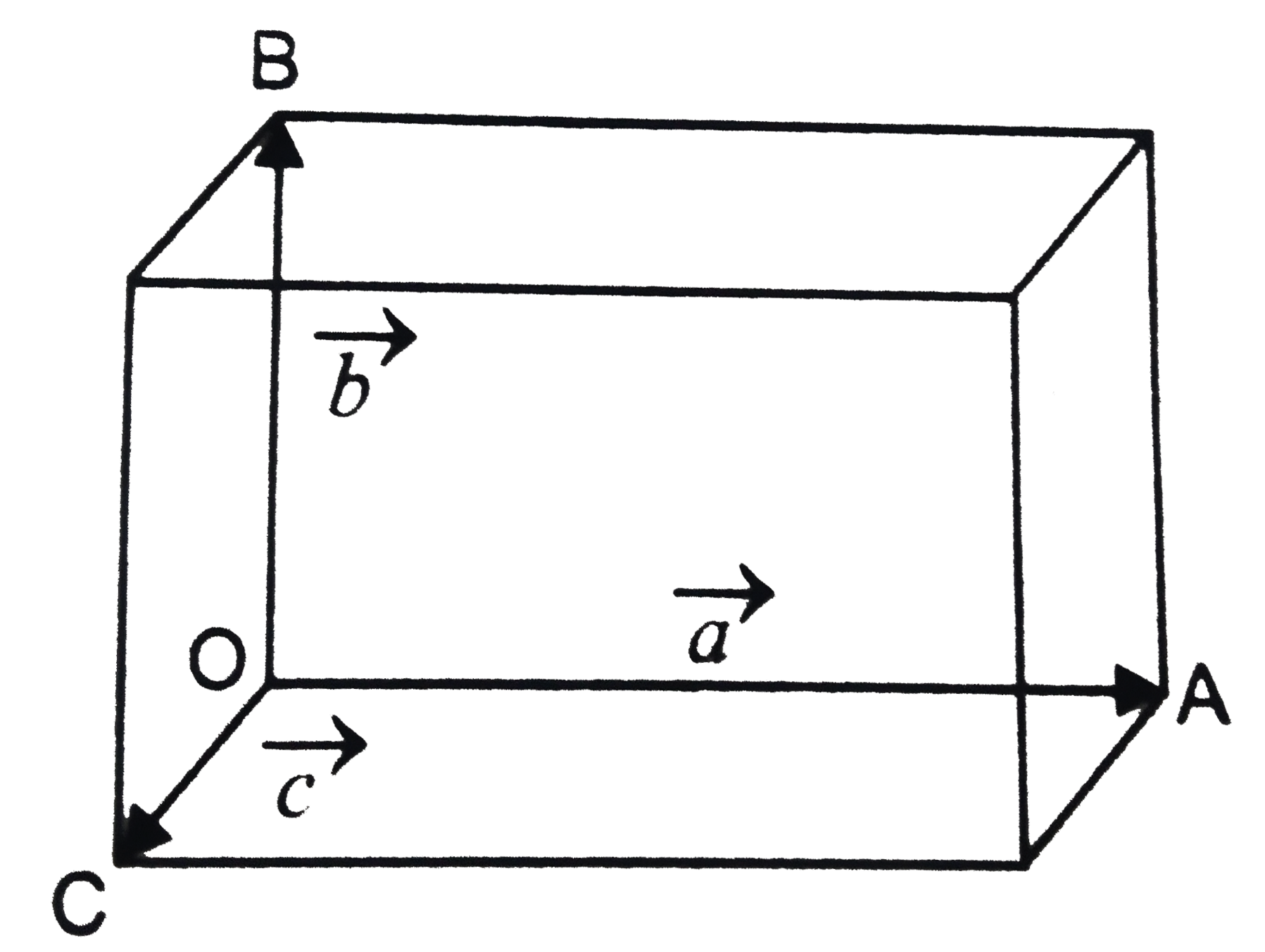
Let a parallelopiped be formed on the three vectors
−−→OA=→a,−−→OB=→b and −−→OC=→c, Fig.
Now, →b×→c=bcsin90∘ˆn=bcˆn
when ˆn is unit vector along −−→OA perpendicular to the plane contaning →b and →c.
Now, →a.(→b×→c)=→a.bcˆn=(a)(bc)cos0∘=abc
which is equal in magnitude to the volume of the parallelopiped.
|
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:QUESTIONS
Explore 15 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADVANCED PROBLEMS FOR COMPETITIONS
Explore 20 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Knowledge Check
Let →C=→A+→B then :
A∣∣→C∣∣ is always greater then ∣∣→A∣∣ and ∣∣→C∣∣<∣∣→B∣∣Bit is possible to haveC∣∣→C∣∣ is always equal to ∣∣→A+→B∣∣D∣∣→C∣∣ is never equal to ∣∣→A+→B∣∣Projection of →P on →Q is :
A→P.ˆQB→P.ˆQC→P׈QD→P׈QWhich of the following is the unit vector perpendicular to ? →A and →B ?
A→A×→BABsinθB→A×→BABcosθC→A×→B∣∣→A.→B∣∣D→A×→B∣∣→A∣∣∣∣→B∣∣
Fill in the blanks :
(i) →τ=→r×… (ii) →L=→r×…
View SolutionTwo vectors →A "and" →B have equal in magnitudes. If magnitudes of →A+→B is equal to n
times the magnitude of →A−→B , then the angle
between →Aand→B is :
View SolutionThe angle between vector (→A×→B) and (→B×→A) is :
View SolutionIf →B=n→A and →A is antiparallel with →B, then n is :
View SolutionThe magnitude of the vector product of two vectors and may be : →A and →B
View Solution

