A car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
To solve the problem, we will follow these steps:
Step 1: Identify the given data
- Weight of the car, m=1800kg
- Distance between the front and back axles, d=1.8m
- Distance of the center of gravity from the front axle, h=1.05m
- Acceleration due to gravity, g=9.8m/s2
Step 2: Calculate the total weight of the car
The total weight W of the car can be calculated using the formula:
W=m⋅g
Substituting the values:
W=1800kg×9.8m/s2=17640N
Step 3: Set up the equilibrium equations
For the car to be in equilibrium:
1. The sum of the vertical forces must equal zero:
N1+N2=W
Where N1 is the normal force on the front wheels and N2 is the normal force on the back wheels.
2. For rotational equilibrium, we can take moments about the front axle:
N2⋅d=W⋅h
Where d is the distance between the axles (1.8 m) and h is the distance from the front axle to the center of gravity (1.05 m).
Step 4: Solve for N2
From the rotational equilibrium equation:
N2⋅1.8=17640⋅1.05
Calculating N2:
N2=17640⋅1.051.8=185221.8≈10290N
Step 5: Solve for N1
Using the vertical forces equilibrium equation:
N1+N2=17640
Substituting N2:
N1+10290=17640
Calculating N1:
N1=17640−10290=7350N
Step 6: Calculate the force on each wheel
Since there are two front wheels and two back wheels:
- Force on each front wheel:
Force on each front wheel=N12=73502=3675N
- Force on each back wheel:
Force on each back wheel=N22=102902=5145N
Final Results
- Force on each front wheel: 3675N
- Force on each back wheel: 5145N
---
- Weight of the car, m=1800kg
- Distance between the front and back axles, d=1.8m
- Distance of the center of gravity from the front axle, h=1.05m
- Acceleration due to gravity, g=9.8m/s2
The total weight W of the car can be calculated using the formula:
W=m⋅g
Substituting the values:
W=1800kg×9.8m/s2=17640N
For the car to be in equilibrium:
1. The sum of the vertical forces must equal zero:
N1+N2=W
Where N1 is the normal force on the front wheels and N2 is the normal force on the back wheels.
N2⋅d=W⋅h
Where d is the distance between the axles (1.8 m) and h is the distance from the front axle to the center of gravity (1.05 m).
From the rotational equilibrium equation:
N2⋅1.8=17640⋅1.05
Calculating N2:
N2=17640⋅1.051.8=185221.8≈10290N
Using the vertical forces equilibrium equation:
N1+N2=17640
Substituting N2:
N1+10290=17640
Calculating N1:
N1=17640−10290=7350N
Since there are two front wheels and two back wheels:
- Force on each front wheel:
Force on each front wheel=N12=73502=3675N
Force on each back wheel=N22=102902=5145N
- Force on each front wheel: 3675N
- Force on each back wheel: 5145N
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:QUESTIONS
Explore 15 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADVANCED PROBLEMS FOR COMPETITIONS
Explore 20 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A car weighs 1800 kg. The distance between its front and back axles is 1·8 m. Its centre of gravity is 1·05 m behind the front axle. Determine the force exerted by the level ground on each front and back wheel
View SolutionA car weighs 1800kg. The distance between its front and back axles is 1.8m. Its centre of gravity is 1.05m behind the front axle. Determine the force (in newton) exerted by the level ground on each front wheel.
View Solution
Knowledge Check
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1 m behind the front axle. The force exerted by the level ground on each front wheel and each back wheel is (Take g:10ms−1)
A4000 N on each front wheel, 5000 N on each back wheelB5000 N on each front wheel, 4000 N an each back wheelC4500N on each front wheel, 4500 N on each back wheelD3000 N on each front wheel, 6000 N on each back wheelThe centre of gravity of a car is at a height h and the distance between its wheel is 2a. The car moves on a level curve of radius r with speed v. Let N1andN2 be the normal reactions on the inner and outer wheels of the car. Then
AN1>N2BN2>N1CN1=N2Dthe maximum value of v to avoid overturning is √arghThe tricycle weighing 20 kg has a small wheel symmmetrically placed 1m behind the two large wheels, which are also 1m apart. If the center of gravity of machine is at a horizontal distance of 25 cm behind the front wheels and the rider whose weight is 40 kg is 10 cm behind the front wheels. Then, the thrust on each front wheel is
A255 NB90 NC200 ND400 N
The radius of the front and rear wheels of a carriage are a and b, and c is the distance between the front an drear axles. A particle of dust driven from the highest point of the rear wheel is observed to alight on the highest point of the front wheel. Find the velocity of the carriage.
View SolutionThere is a man of mass 100 kg sitting on a motorbike of mass 150 kg. The distance of the axles of the wheels (wheelbase) is 1 . 5 m, the common mass center of the man and the motorbike is at a 1 m height above the ground level, and at a 0.6 m distance from the vertical line going through the rear axle.
What acceleration is needed to lift the front wheel?
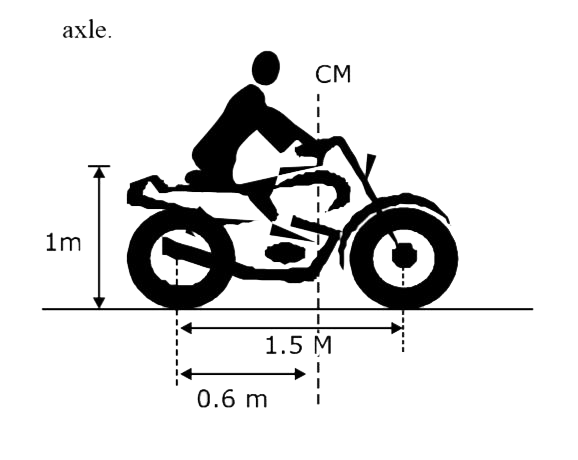
View SolutionThere is a man of mass 100 kg sitting on a motorbike of mass 150 kg. The distance of the axles of the wheels (wheelbase) is 1 . 5 m, the common mass center of the man and the motorbike is at a 1 m height above the ground level, and at a 0.6 m distance from the vertical line going through the rear axle.
What acceleration is needed to lift the front wheel?

View SolutionWhat must be the minimum coefficient of friction μ between the tyres of the drive wheels of a car and the road, if the car and the road, if the car of mass m=2 tons and load M=4 tons, has an acceleration a=0.2ms−2 ? Consider the problem for two cases : (a) all the wheels are driven , (b) only the rear wheels are driven. Assume that the centre of gravity of the car lies at the mid-point between the axes of the wheel and the centre of gravity of the load above the rear axle.
View SolutionA motor car has a width 1.1m between wheels. Its centre of gravity is 0.62 m above the ground and the coefficient of friction between the wheels and the road is 0.8. What is the maximum possible speed, if the centre of gravity inscribes a circle of radius 15 m ? (Road surface is horizontal)
View Solution

