Show that the area of the triangle contained between the vector $\to r and \to b$ is one half of the magnitude of $\to a \times \to b$

Video Solution

Text Solution

Verified by Experts

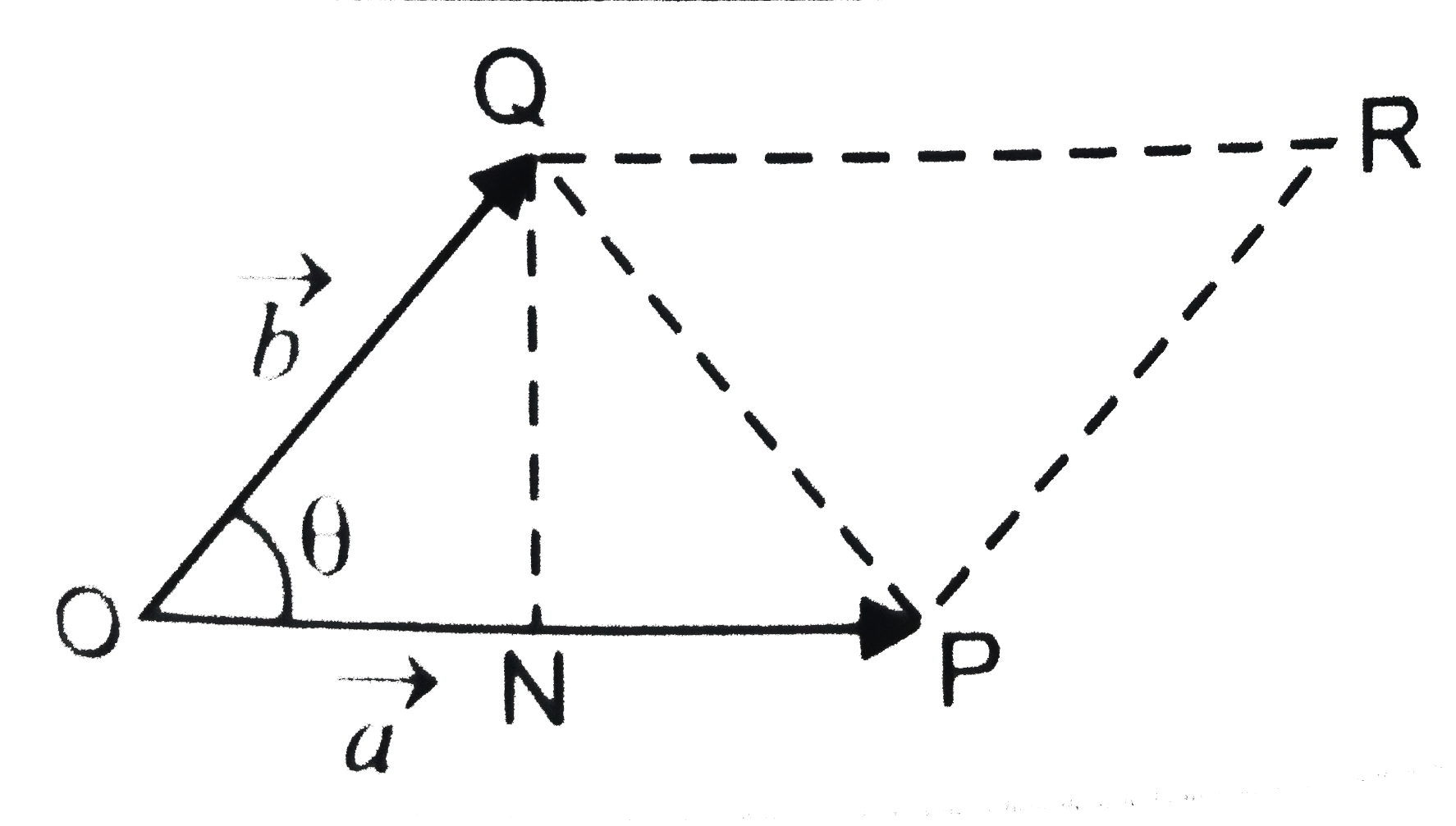
Let $\to a$ be represented by $- - \to O P$ and $\to b$ be represented by $- - \to O Q$ Let $∠ P O Q = θ$ , Fig. Complete the $∣ ∣ g m O P R Q$ . Join $P Q$ .
Draw $Q N ⊥ O P$
In $Δ O Q N, sin θ = \frac{Q N}{O Q} = \frac{Q N}{b}$
$Q N = b sin θ$
now, by defination, $∣ ∣ ∣ \to a \times \to b ∣ ∣ ∣ = a b sin θ = (O P) (Q N) = \frac{2 (O P) (Q N)}{2} = 2 \times$ area of $Δ O P Q$
$∴$ area of $Δ = \frac{1}{2} ∣ ∣ ∣ \to a \times \to b ∣ ∣ ∣$ , which was to be proved.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Projection of $\to P$ on $\to Q$ is :
A $\to P . ˆ Q$
B $\to P . ˆ Q$
C $\to P \times ˆ Q$
D $\to P \times ˆ Q$
Question 2 - Select One
The angle between vector $(\to A - \to B)$ and $(\to B \times \to A)$ is :
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
D $45^{\circ}$
Question 3 - Select One
Two vectors $\to A$ "and" $\to B$ have equal in magnitudes. If magnitudes of $\to A + \to B$ is equal to n
times the magnitude of $\to A - \to B$ , then the angle
between $\to A and \to B$ is :
A ${cos}^{- 1} (\frac{n + n^{2}}{n - n^{2}})$
B ${cos}^{- 1} (\frac{n^{2} + 1}{n^{2} - 1})$
C ${cos}^{- 1} (\frac{n^{2} - 1}{n^{2} + 1})$
D ${cos}^{- 1} (\frac{2 + n}{2 - n})$

PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-NCERT

Home
Ask Doubt
Profile