In the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μu the minimum value of M for which m is at rest is

M=μm2
m=μM2
M=m2μ
m=M2μ
The correct Answer is:A
f+2T
and T=Mg
If m be at rest friction will be static
f≤μN
2Mg≤μmg implies M=μg2 . 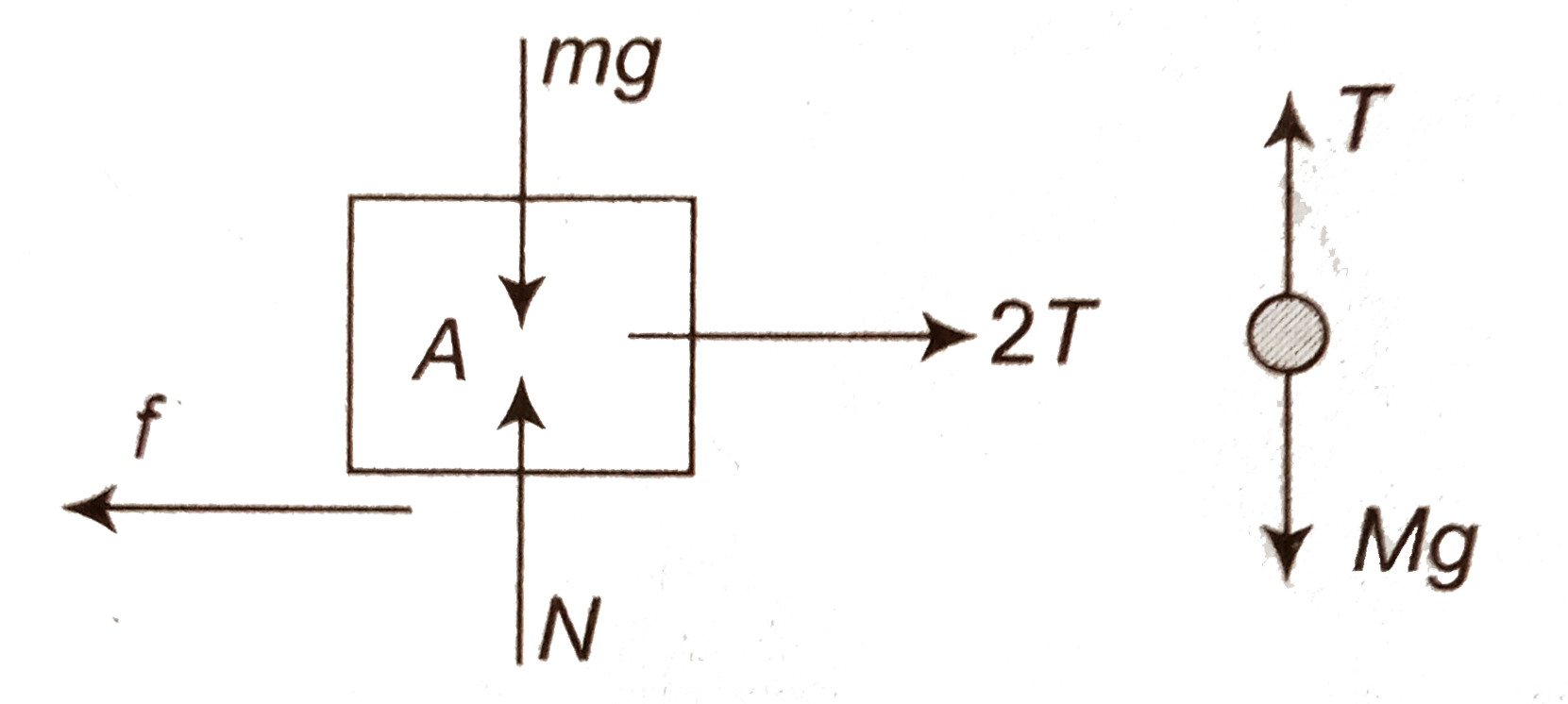
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:NEET Questions
Explore 38 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
When force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ… What should be the minimum value of F so that there is no relative motion between m1andm2
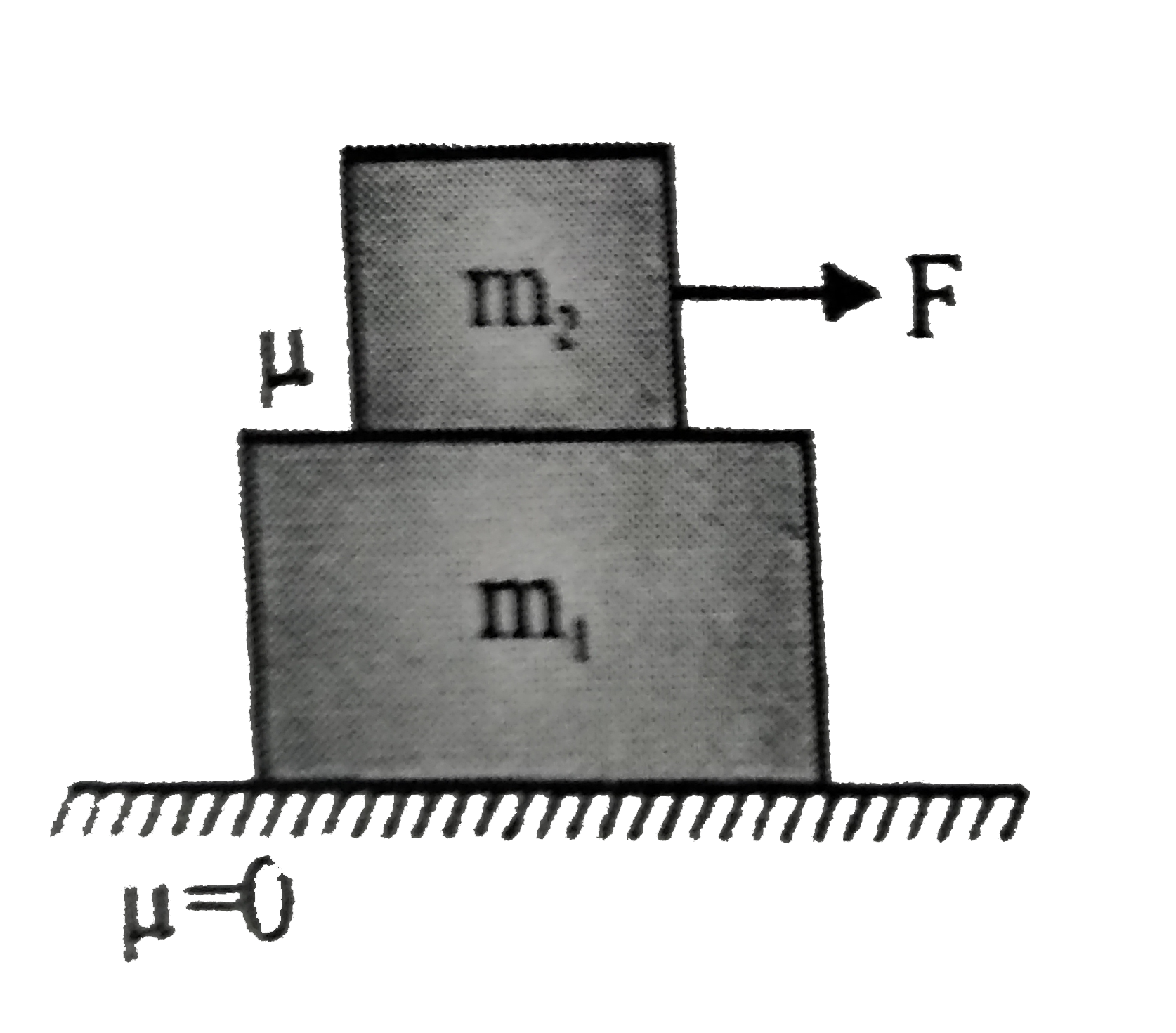
View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

View Solution
Knowledge Check
In the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is
 AM=μm2Bm=μM2CM=m2μDm=M2μ
AM=μm2Bm=μM2CM=m2μDm=M2μIn Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2In the arrangement shown in the figure, the pulley has a mass 3m, Neglecting friction on the contact surface, the force exerted by the supporting rope AB on the ceiling is
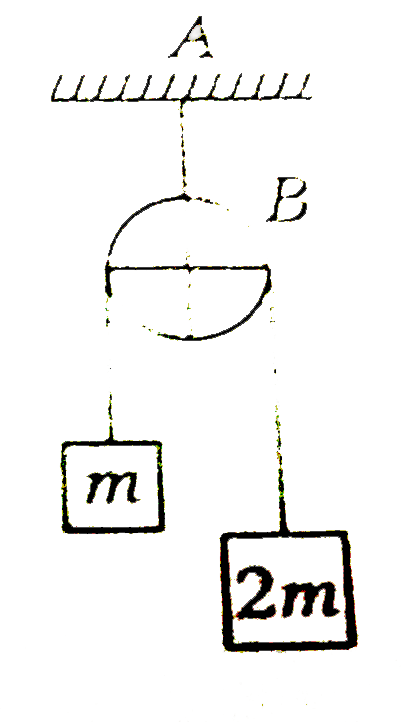 A6 mgB3 mgC4 mgDNone of the above
A6 mgB3 mgC4 mgDNone of the above
Two blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.

View SolutionIn the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
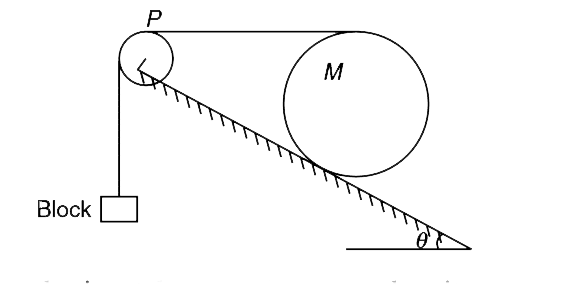
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
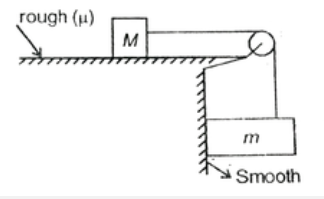
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionIn the system shown in figure the masses of the bodies are known to be m1 and m2, the coefficient of friction between the body m1 and the horizontal plane is equal to k, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment t=0 the body m2 starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body m1 over the first t seconds after the beginning of motion.

View SolutionIn the arrangement shown in figure, pulley and string are light. Friction coefficient between the two blocks is μ whereas the incline is smooth. Block A has mass m and difference in mass of the two blocks isδm. Find minimum value of m for which the system will not accelerate when released from rest.
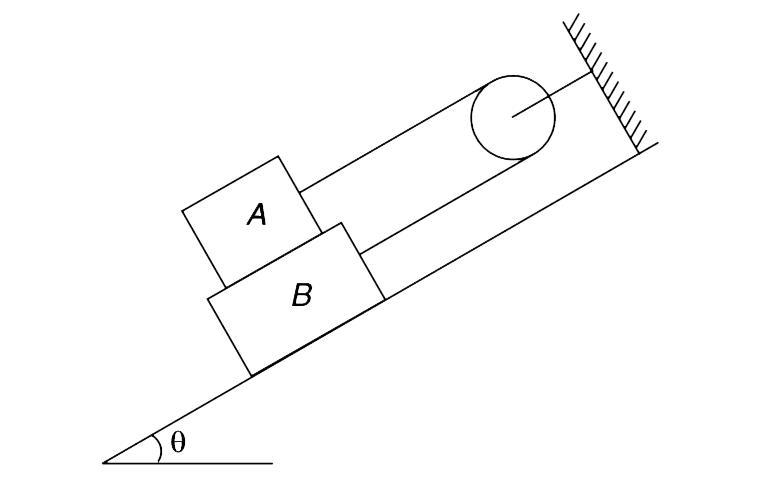
View Solution

