A block placed on a horizontal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started.
μmg(sinθ−μcosθ)
(sinθ−μcosθ)μmg
μmg
none of these
The correct Answer is:A
For vertical equilibrium of the block:
R=Fcosbθ+mg (i)
while for horizontal:
Fsinθ=μr (ii)
From (i) and (ii),
Fsinθ=μ(Fcoshtη+mg)
or F=μmg(sinθ−μcosθ) . 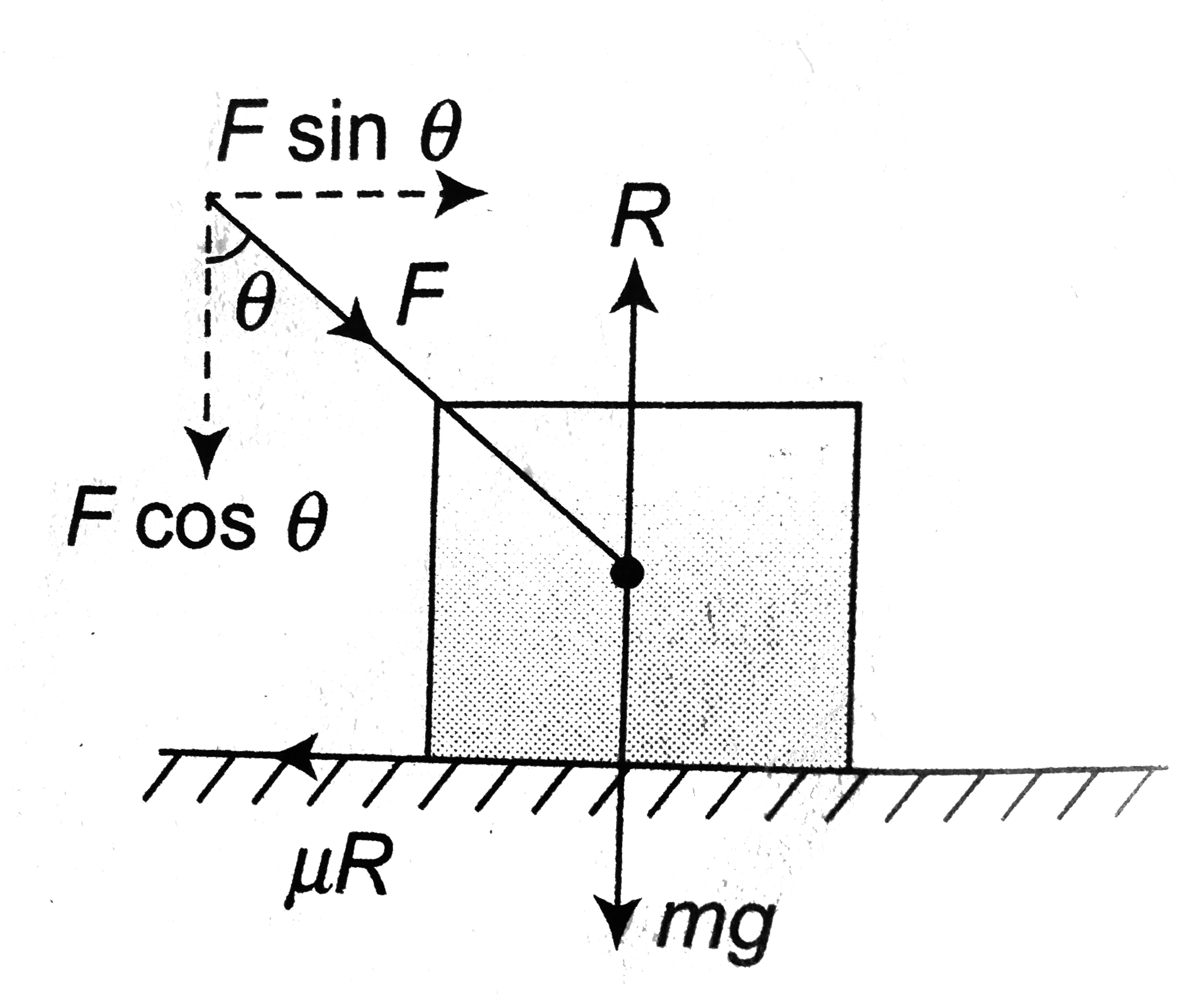
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:NEET Questions
Explore 38 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A block placed on a horizotnal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View SolutionA block placed on a horizotnal surface is being pushed by a force F making an angle θ with the vertical. If the friction coefficient is μ. How much force is needed to get the block just started. Discuss the situation when tanθ<μ.
View Solution
Knowledge Check
A wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
AFM(cosϕ+μsinϕ)−μgBFsin(ϕ)MCμFcosϕD,uFsinϕA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is
 AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−Qcosθ
AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−QcosθA block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
Amgsinϕcos(θ−ϕ)Bmgcosϕcos(θ−ϕ)CmgtanϕDmgsinϕ
A block placed on a horizontal surface is being pushed by a force F making an angle θ with the vertical as shown in Fig. 7.39 . The coefficient of friction between block and surface is μ . (a) Find the force required to slide the block with uniform velocity on the floor . (b) Show that if θ is smaller than a certain

angle θ0 , the block cannot be made to slide across the floor , no matter how great the force be .
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View SolutionA crate is pulled along a horizontal surface at constant velocity by an applied force F that makes an angle θ with the horizontal. The coefficient of kinetic friction between the crate and the surface is μ. Find the angle θ such that the applied force is minimum to slide the block. Also find the minimum value of this force.
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
View Solution

