In the arrangement shown in the figure mass of the block B and A are 2m , 8m respectively. Surface between B floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that the block A remains stationary with respect to B is: (Coefficient of friction between A and B is μ and pulley is ideal).

mμ
2mμ+1
10m1−μ
10mμ−1
The correct Answer is:D
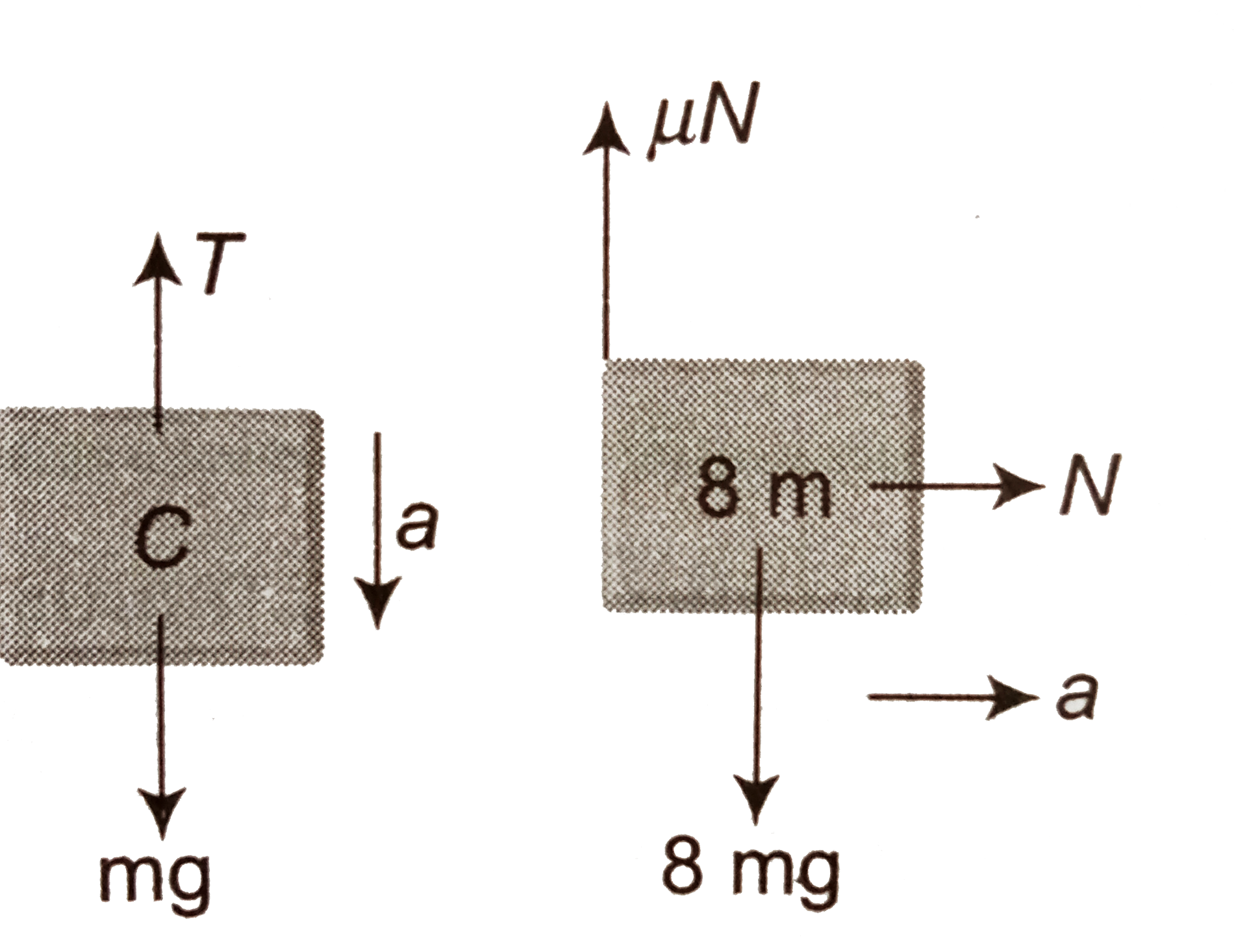
FBD of A
If the acceleration of 'C' is a
For block 'A' N=8ma (1)
8mg−μN=μ8ma (2)
and acceleration a can be written by the equation of system (A+B+C)
m1g=(10m+m1)a (3)
8kmg=μ8m(m1g10m+m1)
10m+m1=μm1
10m=m(μ−1)m1
implies m1=10mμ−1 .
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:NEET Questions
Explore 38 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
The maximum value of the block m2 for which the system will remain in equilibruim (coefficient of friction between block m1 and plane surface is μ, Pulley are mass less ) is :
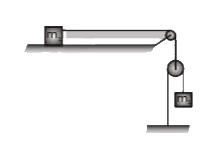
View SolutionTwo block M and and m are arranged as shows in figure . If M=50kg then determine the minimum and maximum value of mass of block the heavy block M stationary

View Solution
Knowledge Check
In the arrangement shown in the figure, mass of the block B and A is 2m and m respectively. Surface between B and floor is smooth. The block B is connected to the block C by means of a string-pulley system. If the whole system is released, then find the minimum value of mass of block C so that A remains stationary w.e.t. B. Coefficient of friction between A and B is μ.
 AmμB2m+1μ+1C3mμ−1D6mμ+1
AmμB2m+1μ+1C3mμ−1D6mμ+1In the given situation, what is the minimum mass of block A so that block B remains stationary with respect to the wall? The coefficient of friction is μ between wall and block. All other surfaces are smooth.
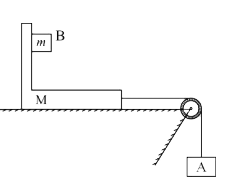 A(M+m)μ+1BMμ−1CM+mμD(M+m)μ−1
A(M+m)μ+1BMμ−1CM+mμD(M+m)μ−1In the arrangement shown in figure, there is a friction force between the blocks of masses m and 2m. The mass of the suspended block is m. The block of mass m is stationary with respect to block of mass 2m. The minimum value of coefficient of friction between m and 2m is
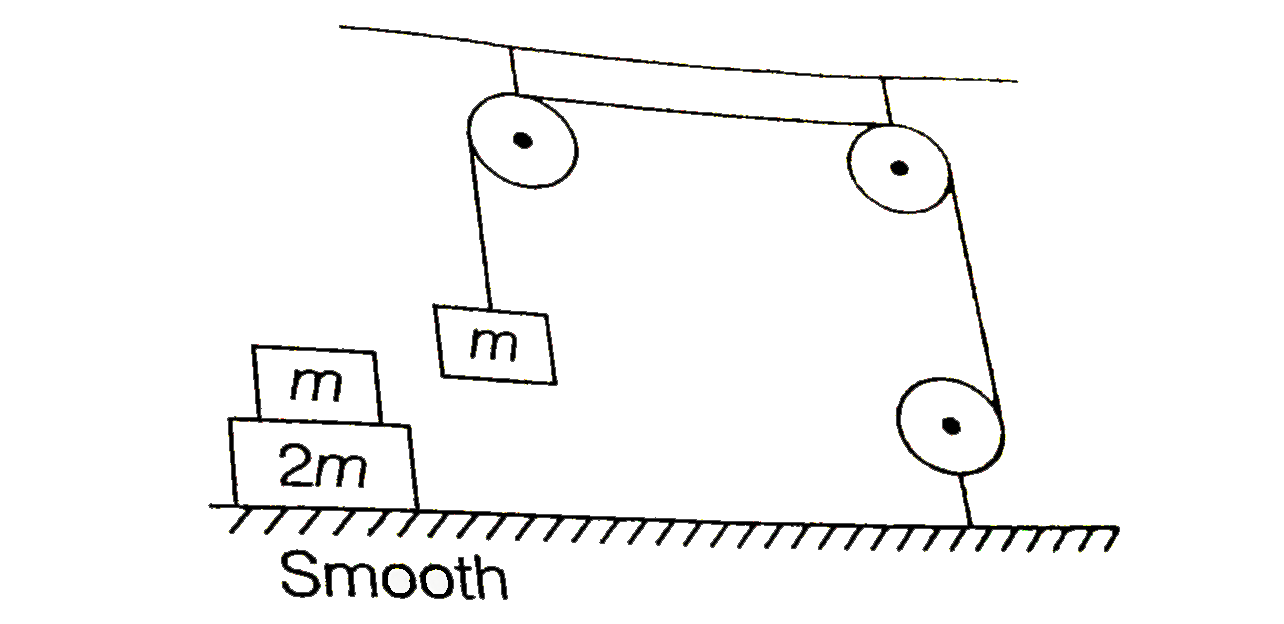 A12B1√2C14D13
A12B1√2C14D13
Three blocks are placed as shown in figure. Mass of A, B and C are m1,m2,and m3respectively. The force exerted by block 'C' on 'B' is :-
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.

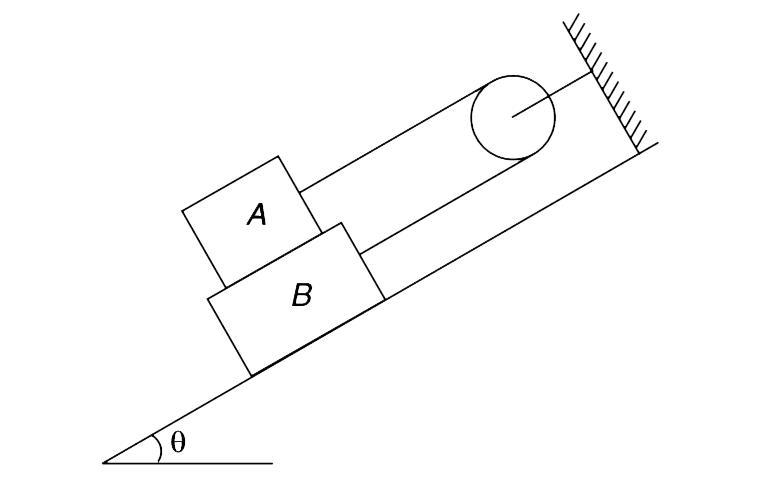
View SolutionIn the arrangement shown in figure, pulley and string are light. Friction coefficient between the two blocks is μ whereas the incline is smooth. Block A has mass m and difference in mass of the two blocks isδm. Find minimum value of m for which the system will not accelerate when released from rest.
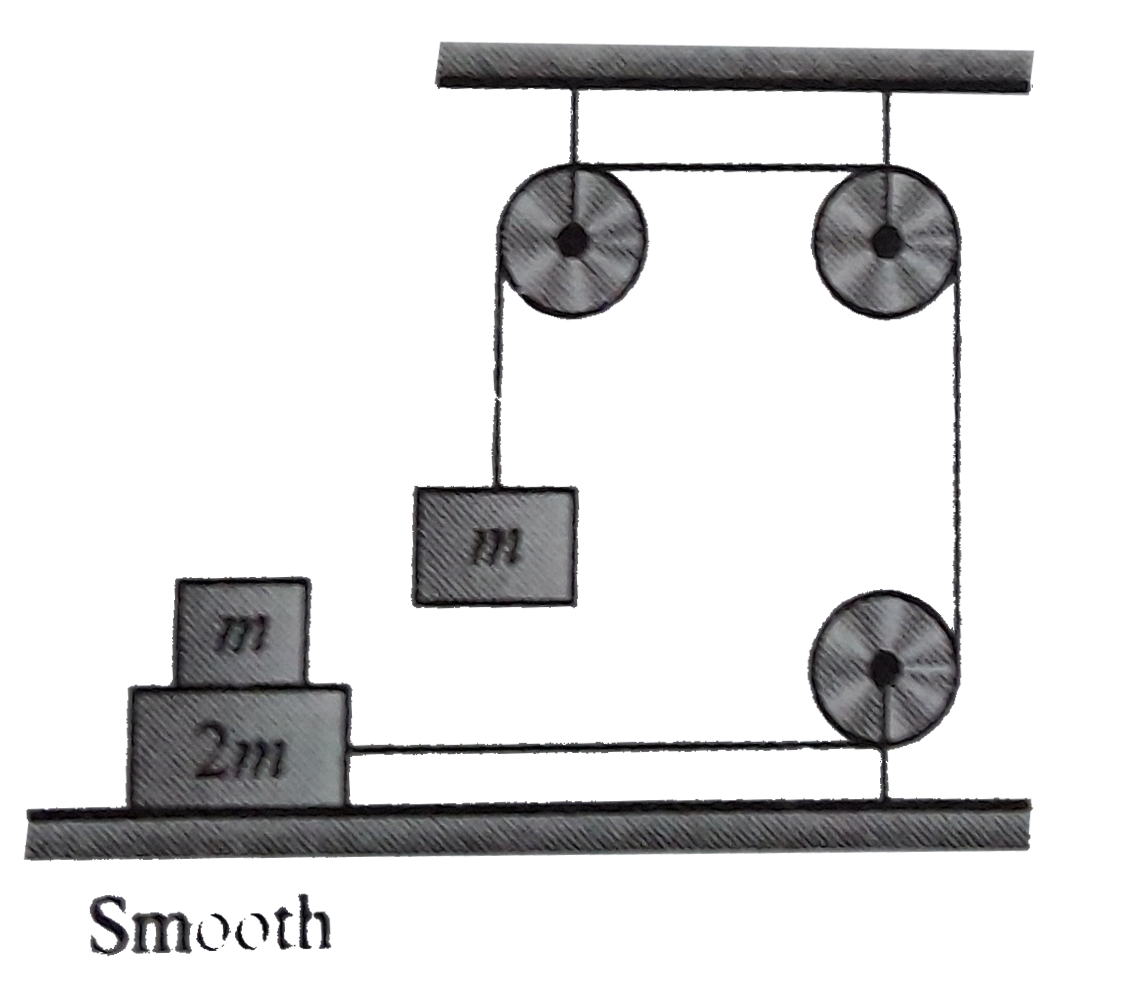
View SolutionIn the arrangement shown in Fig there is no friction between of mass 2m and ground but there is friction between the block of masses m is stationary with respect to block of mass 2m The value of friction between m and 2mis
View SolutionIn the diagram shown, the block A and B are of the same mass M and the mass of the block C is (M1). Friction is present only under the block A. the whole system is suddenly released from the state of rest. The minimum coefficient of friction on keep the block A in the state of rest is equal to .

View Solution