The ratio of tensions in the string connected to the block of mass m2 in figure, respectively, is (friction is absent everywhere):[m1=50kg,m2=80kg and F=1000N] ![The ratio of tensions in the string connected to the block of mass m(2) in figure, respectively, is (friction is absent everywhere):[m(1)=50 kg, m(2)=80kg and F=1000N]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_CA1_E01_011_Q01.png)
7:2
2:7
3:4
4:3
The correct Answer is:C
In figure (i): Let tension in the string is T1
F−T1=m1a
implies 1000−T1=50a (1)
T1−m2g=m2a
implies T1−80g=80a (2)
From (1) and (2) T1=12,00013N
In figure (ii): Let tension in the string is T2 .
F+m1g−T2=m1a
⇒1000+50g−T2=50a (3)
T2−80g=80a (4)
From (3) and (4)
T2=1600013N⇒T1T2=1200016000=34 .
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Assertion Reasoning
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - NEET Questions
38 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Dynamics Of Circular Motion
31 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
Find the mass M so that it remains at rest in the abjoining figure. Both the pulley and string are light and friction is absent everywhere. (g=10m/s2)

View SolutionAs shown in Fig. three blocks connected together lie on a horizontal frictionless table and pulled to the right with a force F = 50 N. If m1=5kg,m2=10kg and m3=15kg, find the tensions T1 and T2.

View Solution
Knowledge Check
In each of the three arrangements, the block of mass m1 is being pulled left with constant velocity. There is no friction anywhere. The string are light and anextensible and pulleys are massless. The ratio of the speed of the block of mass m2 in the three cases respectively is:
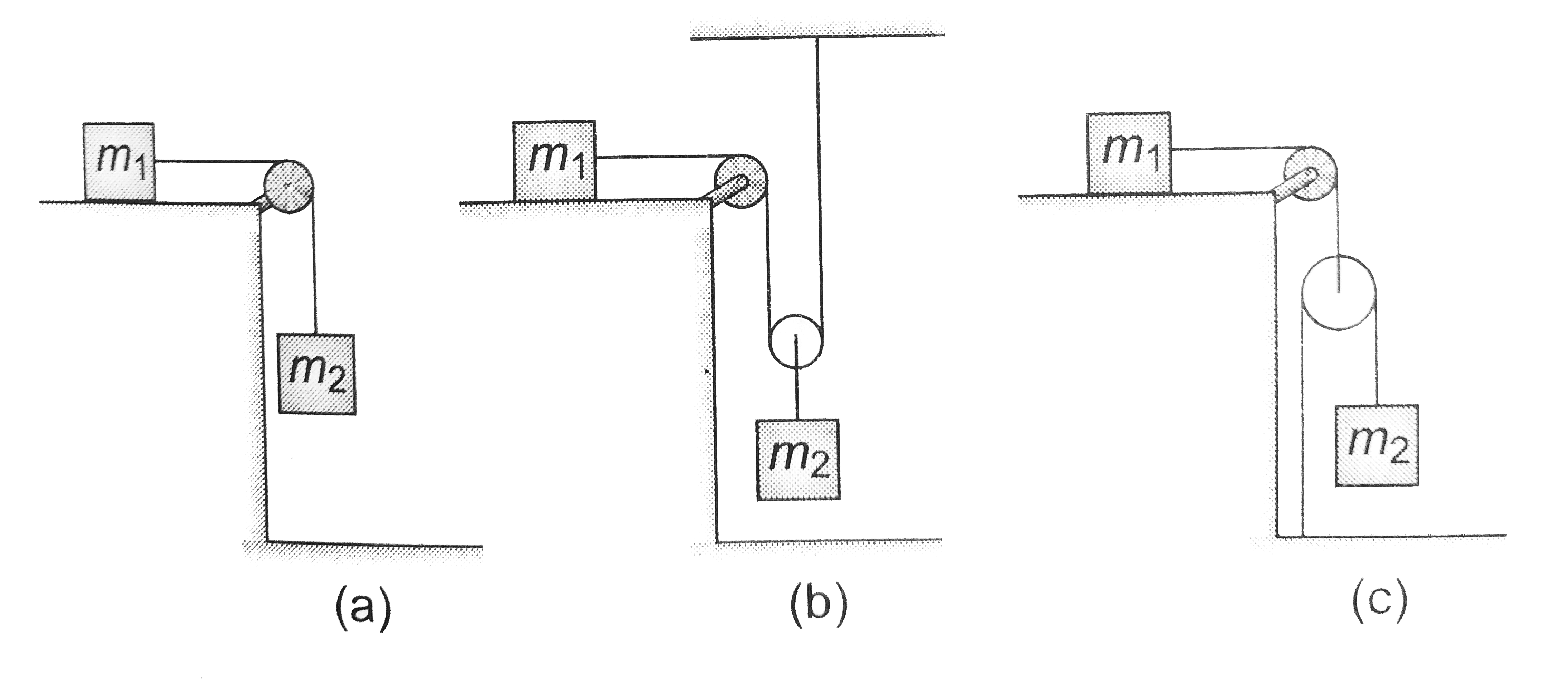 A2:1:4B2:4:1C4:2:1DConnot be calculated
A2:1:4B2:4:1C4:2:1DConnot be calculatedThree blocks are connected as shown in figure on a horizontal frictionless table. If m1=1kg , m2=8kg , m3=27kg and T3=36N , T2 will be.
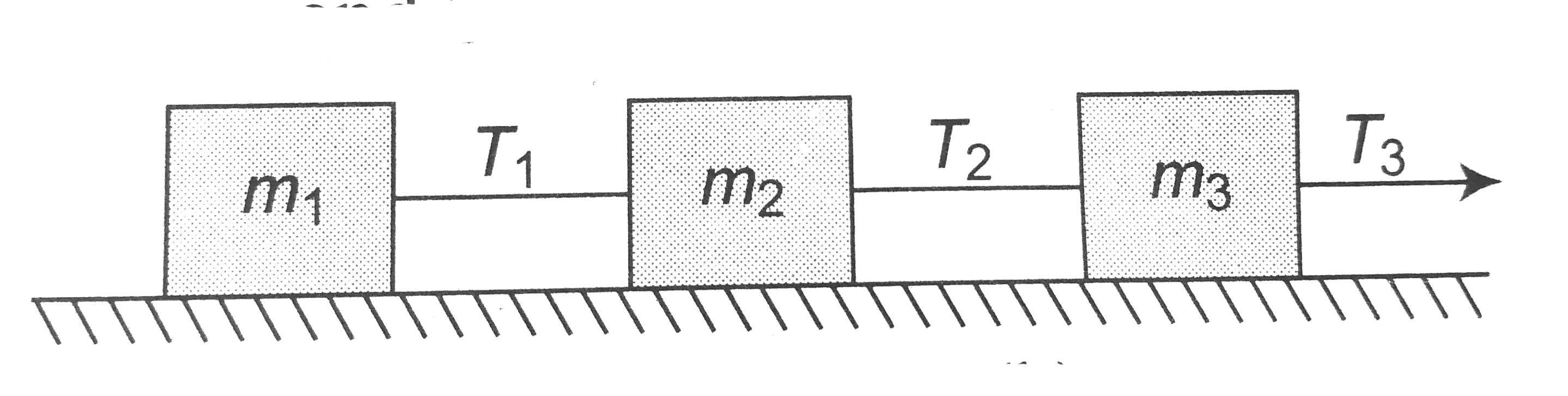 A18NB9NC3.375ND1.75N
A18NB9NC3.375ND1.75NTwo blocks of masses m and M are connected by an inextensible light string as shown in the figure. When a constant horizontal force F acts on the block of the mass M, then tension in the string is : (Assume that constact between the ground and the two blocks are frictionless) and blocks will not topple. (Given: m=1kg,M=4kg,F=10N,θ=60∘)
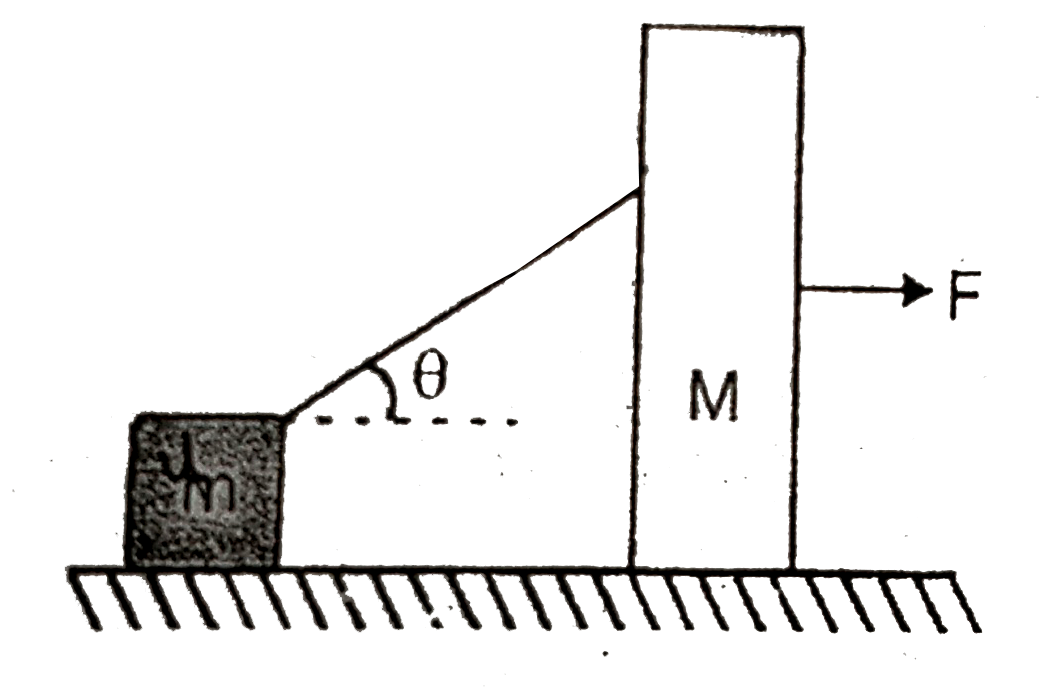 A1NB2NC4ND3N
A1NB2NC4ND3N
The block C shown in the figure is ascending with an acceleration a=3m/s2 by means of some motor not shown here. Find the acceleration of the bodies A and B of masses 10kg and 5kg respectively in m/s2, assuming pulleys are massless and friction is absent everywhere.
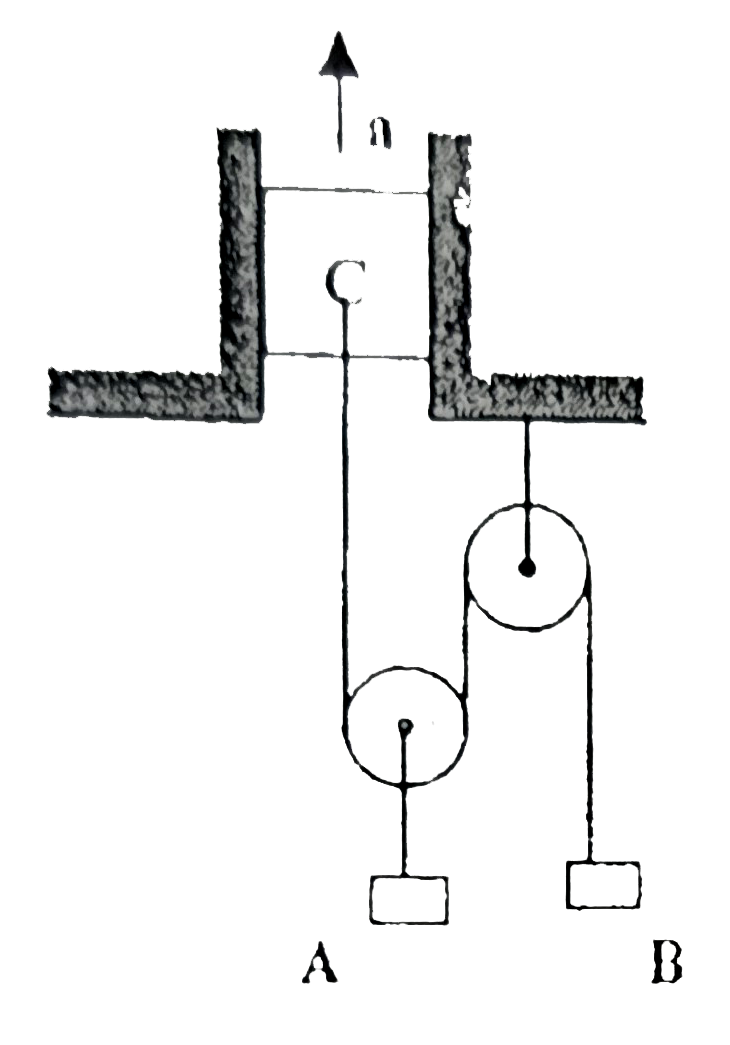
View SolutionTwo blocks are connected by a massless string that passes over a frictionless peg as shown in Fig. 3E.46. One end of the string is attached to a mass m1=3kg i.e. a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3 kg block be released in order to just lift the 6 kg block off the table ?
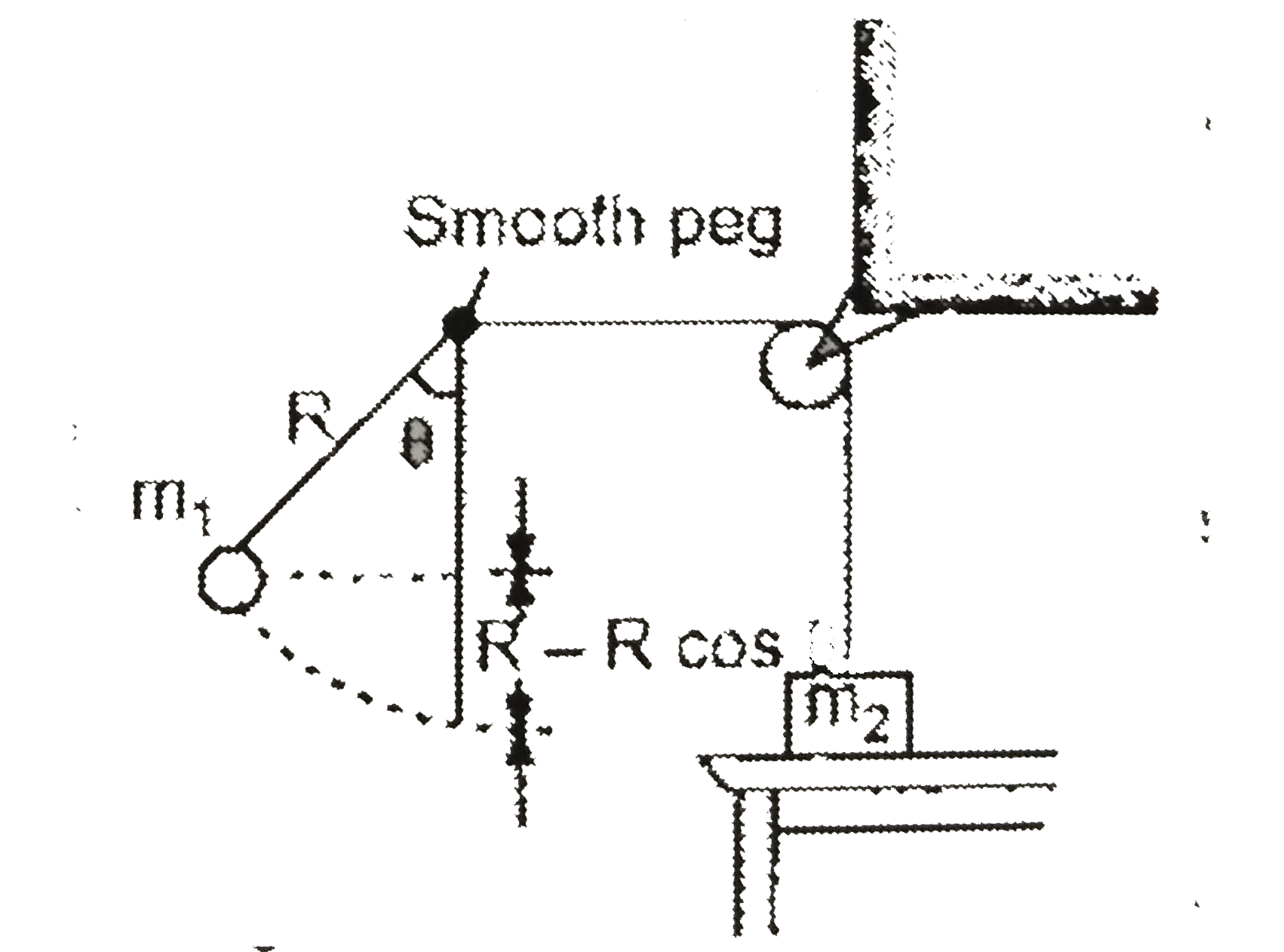
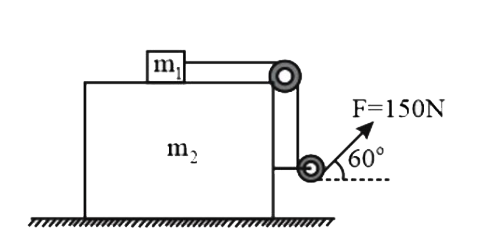
View SolutionIn the arrangement shown in the figure, friction exists only between the two blocks, A and B. The coefficient of static friction μs=0.6 and coefficient of kinetic friction μk=0.4, the masses of the blocks A and B are m1=20kg and m2=30kg, respectively. Find the acceleration (in ms−2) of m1, if a force F=150N is applied, as shown in the figure. [Assume that string and pulleys are massless]
View SolutionThree blocks are connected as shown in fig. on a horizontal frictionless table if m1=1kg,m2=8kg,m3=27kg and T3=36N,T2 will be:-

View SolutionThree blocks of masses m1,m2andm3 are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, then tension T2 will be

View Solution
