Question

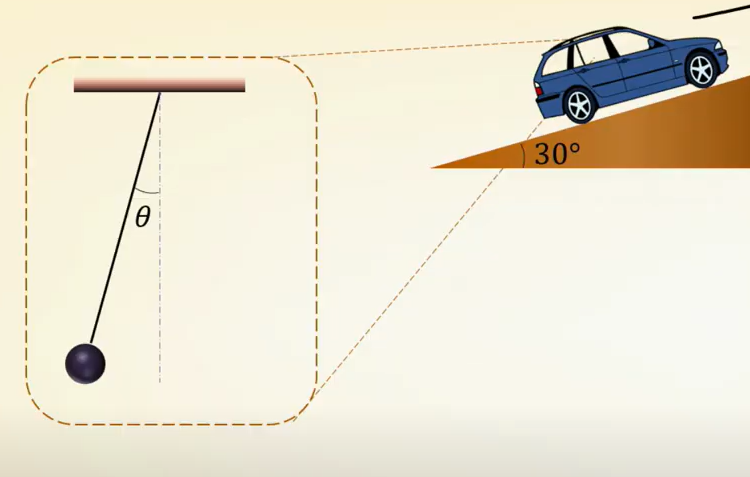
A car is moving on a plane inclined at ${30}^{\circ }$ to the horizontal with an acceleration of $10m/s^2$ parallel to the plane upward. A bob is suspended by a string from the roof. The angle in degrees which the string makes with the vertical is: (Assume that the bob does not move relative to car) $[g=10m/s^2]$

Options

A. `20^(@)`
B. `30^(@)`
C. `45^(@)`
D. `60^(@)`

Answer

B

Explanation

To solve the problem, we will analyze the forces acting on the bob suspended from the roof of the car that is moving on an inclined plane. Here are the steps to find the angle α that the string makes with the vertical:

Step 1: Identify the Forces Acting on the Bob
The forces acting on the bob are:
1. The gravitational force (weight) acting downward, \( F_g = mg \).
2. The tension in the string, \( T \), acting along the string.
3. A pseudo force acting horizontally due to the car's acceleration, \( F_p = ma \), where \( a = 10 \, \text{m/s}^2 \).

Step 2: Resolve the Forces
Since the car is inclined at \( 30^\circ \) to the horizontal, we need to resolve the forces into components. The pseudo force can be resolved into two components:
- Along the incline: \( F_{p,\parallel} = F_p \sin(30^\circ) = ma \cdot \frac{1}{2} = 5m \)
- Perpendicular to the incline: \( F_{p,\perpendicular} = F_p \cos(30^\circ) = ma \cdot \frac{\sqrt{3}}{2} = 5m\sqrt{3} \)

The weight of the bob can also be resolved:
- Perpendicular to the incline: \( F_{g,\perpendicular} = mg \cos(30^\circ) = mg \cdot \frac{\sqrt{3}}{2} \)
- Along the incline: \( F_{g,\parallel} = mg \sin(30^\circ) = mg \cdot \frac{1}{2} \)

Step 3: Write the Equations of Motion
In the frame of the car (non-inertial frame), the bob is in equilibrium, so the net forces in both directions must balance.

1. Along the incline:
\( T \sin(\alpha) = mg \sin(30^\circ) + 5m \)
\( T \sin(\alpha) = \frac{mg}{2} + 5m \)

2. Perpendicular to the incline:
\( T \cos(\alpha) = mg \cos(30^\circ) + 5m\sqrt{3} \)
\( T \cos(\alpha) = mg \cdot \frac{\sqrt{3}}{2} + 5m\sqrt{3} \)

Step 4: Divide the Equations
To eliminate \( T \), we can divide the two equations:
\( \frac{T \sin(\alpha)}{T \cos(\alpha)} = \frac{\frac{mg}{2} + 5m}{\frac{mg \sqrt{3}}{2} + 5m\sqrt{3}} \)
This simplifies to:
\( \tan(\alpha) = \frac{\frac{g}{2} + 5}{\frac{g \sqrt{3}}{2} + 5\sqrt{3}} \)

Step 5: Substitute Values
Substituting \( g = 10 \, \text{m/s}^2 \):
\( \tan(\alpha) = \frac{\frac{10}{2} + 5}{\frac{10 \sqrt{3}}{2} + 5\sqrt{3}} = \frac{5 + 5}{5\sqrt{3} + 5\sqrt{3}} = \frac{10}{10\sqrt{3}} = \frac{1}{\sqrt{3}} \)

Step 6: Find the Angle α
Thus, we have:
\( \alpha = \tan^{-1}\left(\frac{1}{\sqrt{3}}\right) = 30^\circ \)

Final Answer
The angle which the string makes with the vertical is \( 30^\circ \).

---