In the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is $μ = 0.5$ . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

$25 N$

$40 N$

$30 N$

$20 N$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

In the arrangement shown in figure $m_{A} = m_{B} = 2 k g$ . String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient between blocks A and B is $μ = 0.5$ . What maximum horizontal force F can be applied so that block A does not slip over the block B? $(g = 10 m / s^{2})$

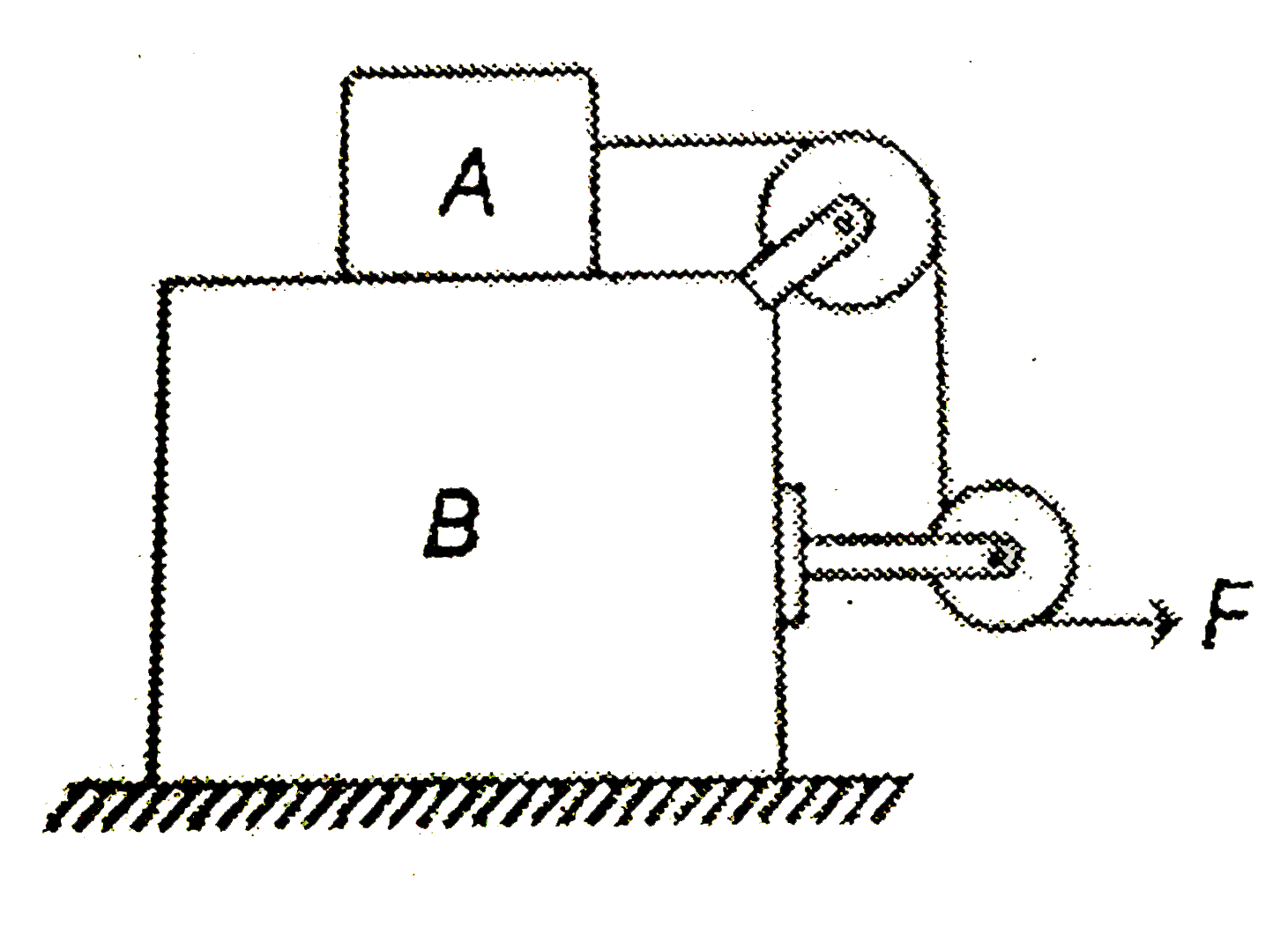A25 N
B40 N
C30 N
D20 N
Two block A and B of masses 5 kg. and 3 kg. respectively rest on smooth horizontal surface with B over A. The coefficient of friction between A and B. 0.5 the maximum horizontal force that can be applied to A so that there will be motion of A and B without separation is :-
A15
B25
C40
D50
A block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface $(μ) = 0.5 .$ A horizontal force F is acting on the block. When

AF = 4 N, acceleration is zero.
BF = 4 N, friction is 10 N and acceleration is $3 m / s^{2} .$
CF = 14 N, acceleration is $2 m / s^{2} .$
DF = 14 N, friction is 14 N.