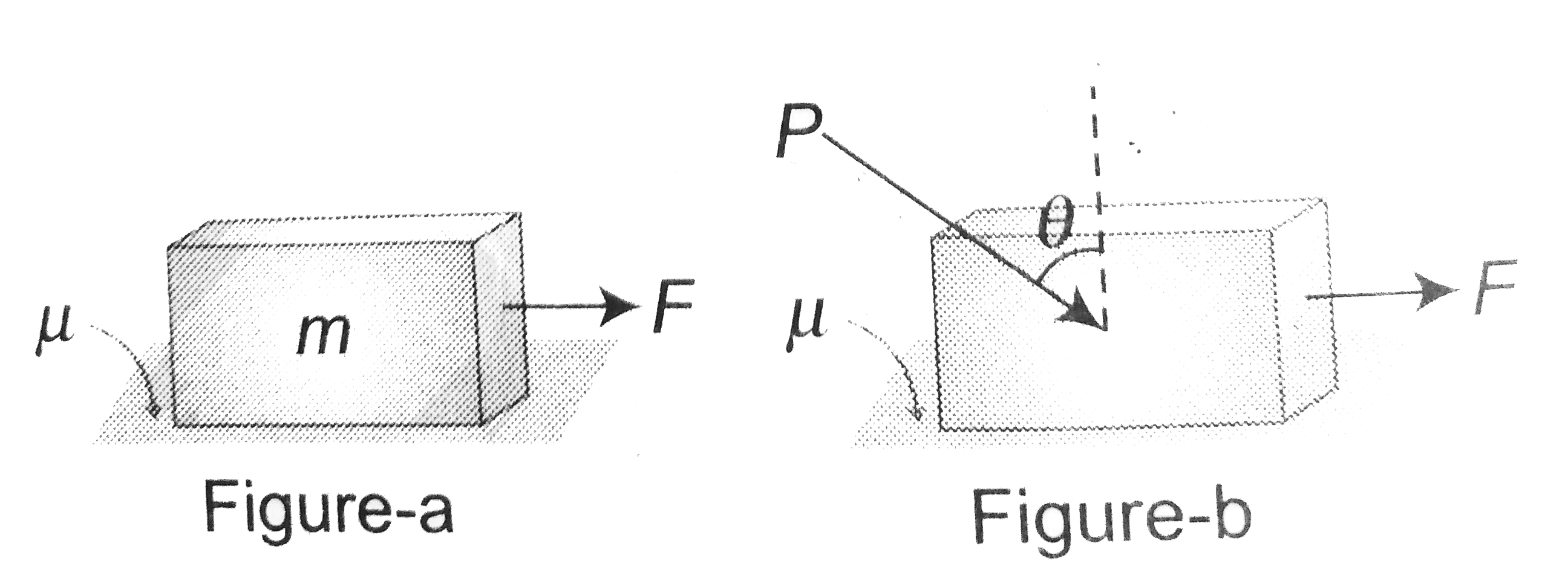
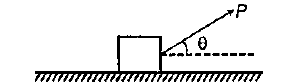
The coefficient of friction between the block and the horizontal surface is mu. The block moves toward right under action of horizontal force F (figure-a). Sometime later another force P is applied to the block making an angle theta (suchtˆtanθ=μ) with vertical as shown in (figure-b). After application of force P , the acceleration of block shall.
Increases
Decrease
remains same
information insufficient for drawing inference.
The correct Answer is:C
The free body diagram of block in fig. b is as shown.
:. N=mg+Pcosθ
and acceleration of block
a=F+Psinθ−μ(mg+Pcoshθ)m
a=F+Psinθ−sinθcosθ(mg+Pcoshθ)m=F−μmgm Hence P does not change acceleration. 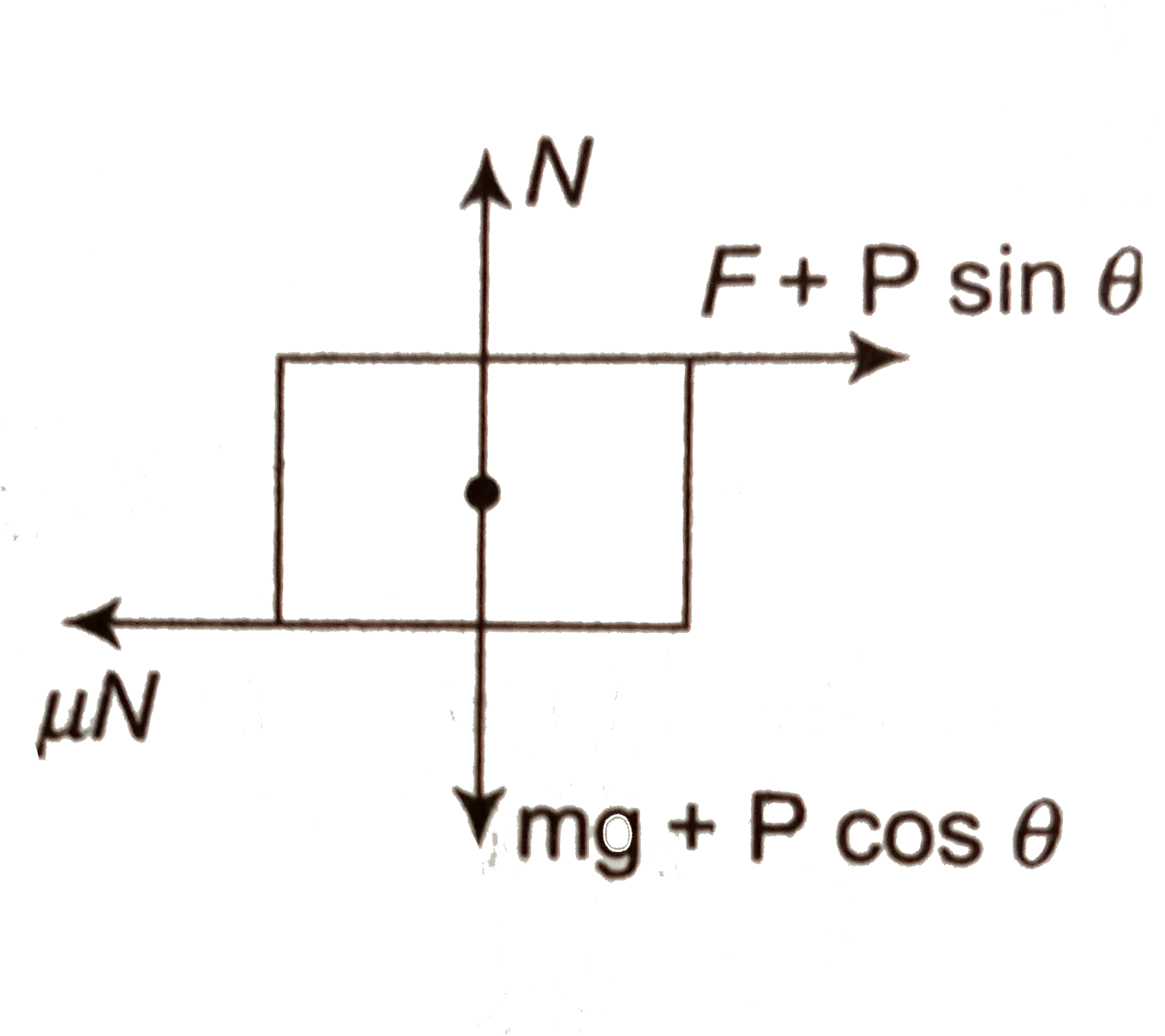
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:NEET Questions
Explore 38 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionThe friction coefficient between the blocks is μ. If force F is applied on the lower block , analyse motion of two blocks.

View Solution
Knowledge Check
In Fig. 7.149 , coefficient of friction between the block and the floor is μ . Force F that will move the block on the floor with a uniform speed is :
 A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθ
A(μsinθ+cosθ)mgB(μsinθ−cosθ) mgCμmgcosθ−μsinθDμmgsinθ−μcosθIn the arrangement shown in figure, coefficient of friction between the two blocks is μ=1/2. The force of friction acting between
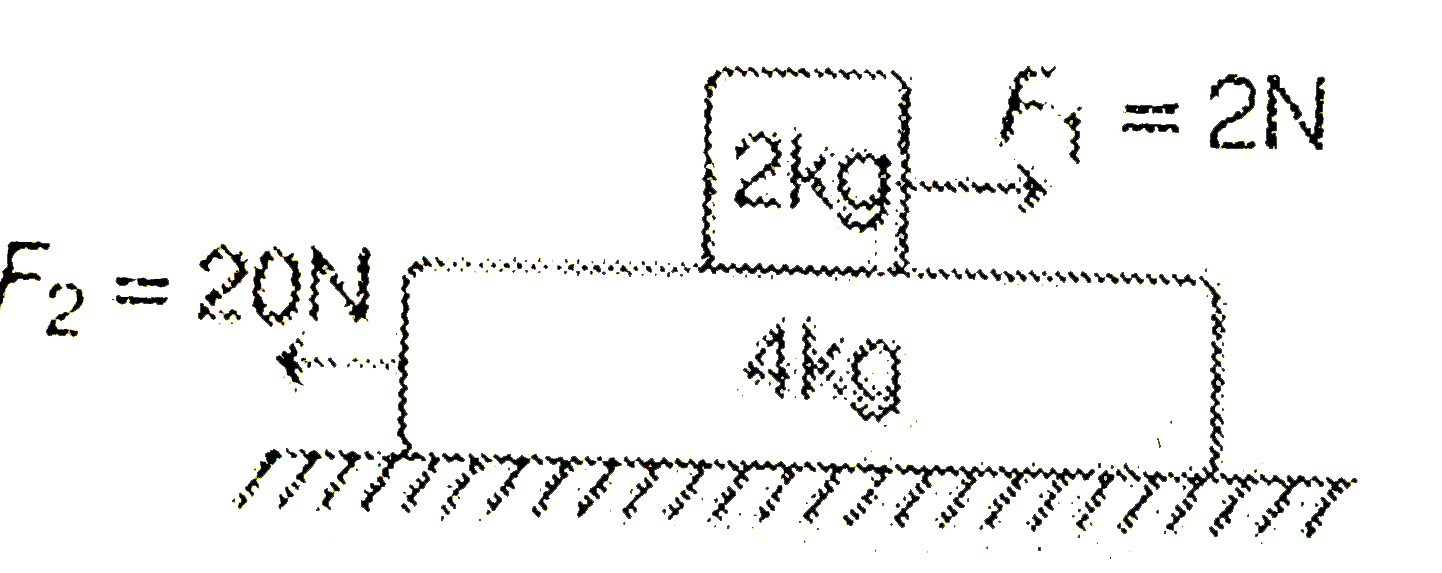 A8NB10NC6ND4N
A8NB10NC6ND4NA block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθ
A block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
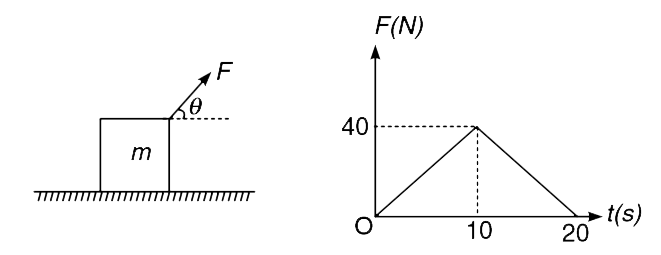
View SolutionA block of mass m=4.4kg lies on a horizontal rough surface. The coefficient of friction between the block and the surface is μ=0.5. A force F starts acting on the block making an angle θ=37∘ to the horizontal. The force changes with time as shown in the graph.
(a) At what time the block begins to move ?
(b) Calculate the maximum speed attained by the block.
[tan37∘=34,g=10ms−2]
View SolutionIn the situration shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are
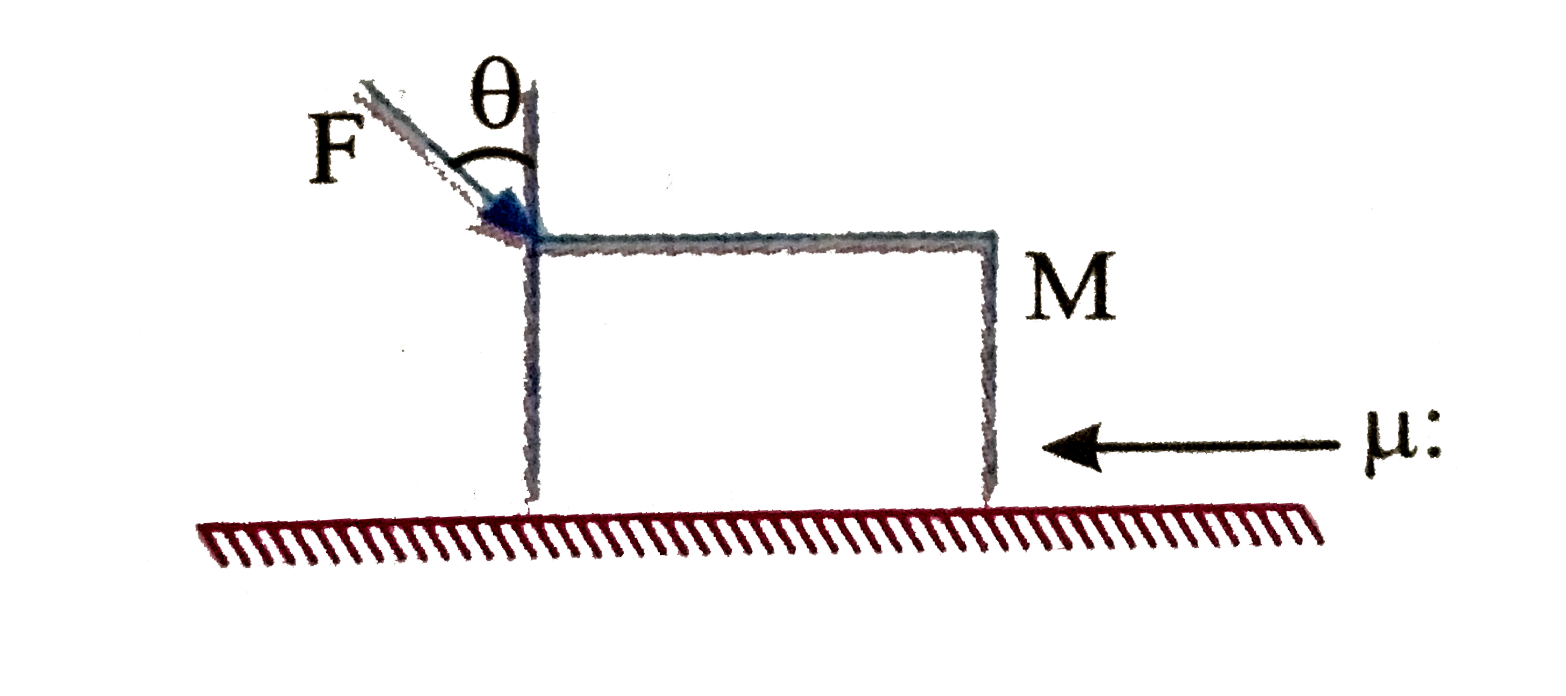
View SolutionIn the situatiobn shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are :

View SolutionA block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.
View Solution

