A small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle 'a' with the vertical in equilibrium. Then the tension in the string is :
m√a2+g2
ma√a2+g2
mgsinθ
mgcosθ
The correct Answer is:A
To find the tension in the string when the ball is in equilibrium and the string makes an angle θ with the vertical as the car accelerates, we can follow these steps:
Step 1: Identify the Forces Acting on the Ball
When the car accelerates, two forces act on the ball:
1. The gravitational force (weight) acting downward: Fg=mg
2. The pseudo force acting horizontally due to the car's acceleration: Fp=ma
Step 2: Analyze the Forces in the Equilibrium Condition
In equilibrium, the ball is not accelerating, which means the net force acting on it is zero. The tension T in the string must balance these forces. The tension can be resolved into two components:
- A vertical component Tcos(θ) that balances the weight mg.
- A horizontal component Tsin(θ) that balances the pseudo force ma.
Step 3: Set Up the Equations
From the vertical forces:
Tcos(θ)=mg (1)
From the horizontal forces:
Tsin(θ)=ma (2)
Step 4: Divide the Two Equations
To eliminate T, we can divide equation (2) by equation (1):
Tsin(θ)Tcos(θ)=mamg
This simplifies to:
tan(θ)=ag
Step 5: Solve for Tension T
Now, we can express T in terms of mg and θ:
From equation (1):
T=mgcos(θ)(3)
Step 6: Substitute tan(θ) into the Tension Equation
Using tan(θ)=ag, we can find cos(θ):
cos(θ)=g√g2+a2
Substituting this back into equation (3):
T=mgg√g2+a2=mg⋅√g2+a2g=m√g2+a2
Final Answer
Thus, the tension in the string is:
T=m√g2+a2
When the car accelerates, two forces act on the ball:
1. The gravitational force (weight) acting downward: Fg=mg
2. The pseudo force acting horizontally due to the car's acceleration: Fp=ma
In equilibrium, the ball is not accelerating, which means the net force acting on it is zero. The tension T in the string must balance these forces. The tension can be resolved into two components:
- A vertical component Tcos(θ) that balances the weight mg.
- A horizontal component Tsin(θ) that balances the pseudo force ma.
From the vertical forces:
Tcos(θ)=mg (1)
Tsin(θ)=ma (2)
To eliminate T, we can divide equation (2) by equation (1):
Tsin(θ)Tcos(θ)=mamg
This simplifies to:
tan(θ)=ag
Now, we can express T in terms of mg and θ:
From equation (1):
T=mgcos(θ)(3)
Using tan(θ)=ag, we can find cos(θ):
cos(θ)=g√g2+a2
Substituting this back into equation (3):
T=mgg√g2+a2=mg⋅√g2+a2g=m√g2+a2
Thus, the tension in the string is:
T=m√g2+a2
Similar Questions
A pedulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road Find the angle made by the string with vertical at equilibrium Also find the tension in the string in this position
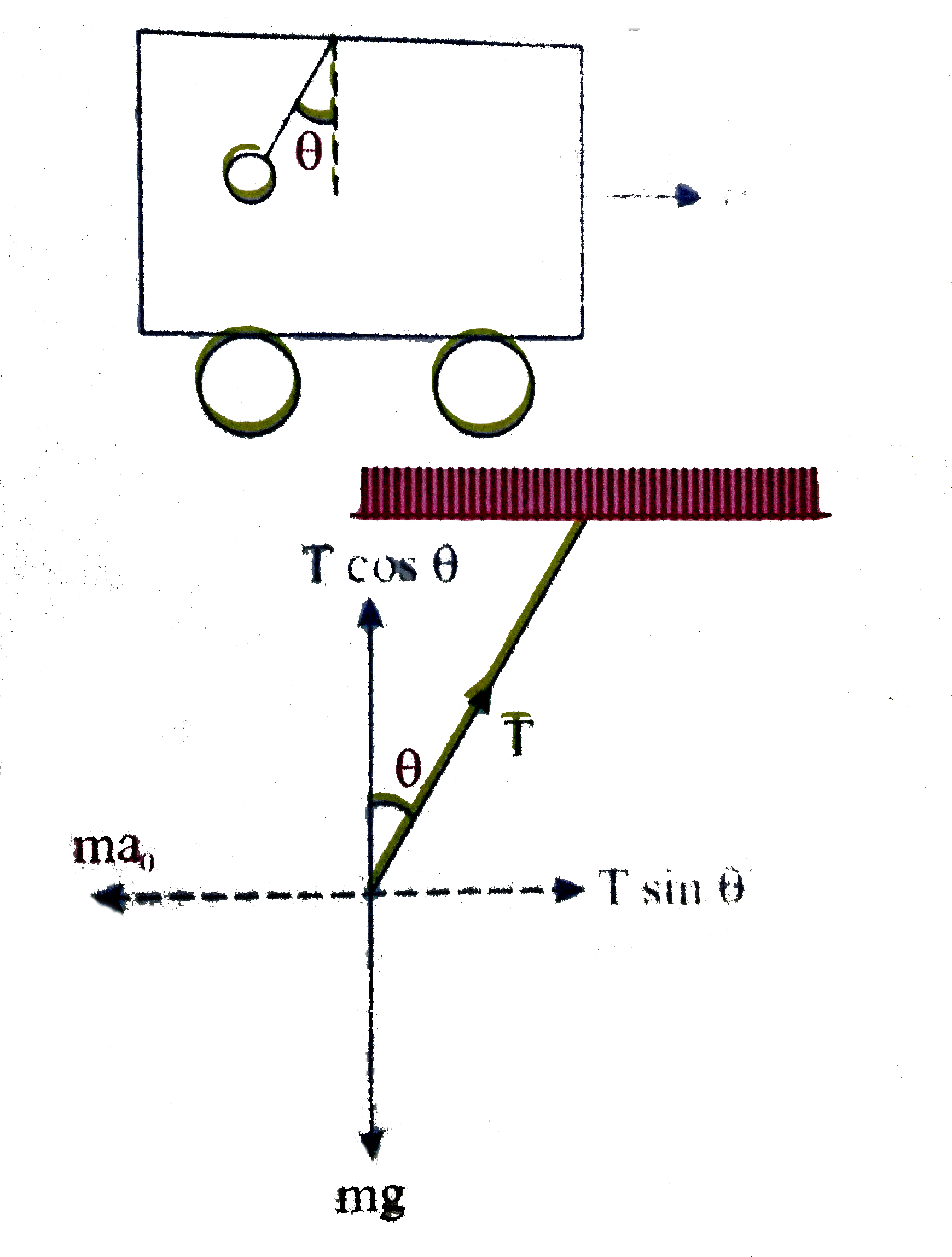 .
.
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with to the road. Find the angle made by the string with the verical and tension in the string.
View Solution
Knowledge Check
A plumb bob is hanging from the ceiling of car. If the car move with acceleration a, the angle made by the string with the vertical is
Atan−1(ag)Btan−1(ga)Ccos−1(ga)Dcos−1(ag)A small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
Atan−1(a/g) in the direction of motionBtan−1(a/g) opposite to the direction of motionCtan−1(g/a) in the direction of motionDtan−1(g/a) opposite to the direction of motionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
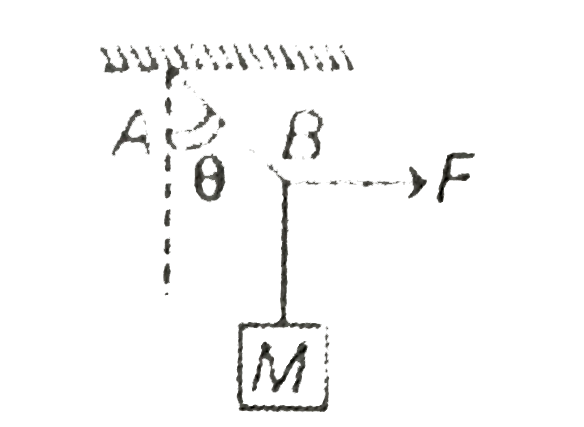 AF sinθBF/sinθCFcosθDF/cosθ
AF sinθBF/sinθCFcosθDF/cosθ
A pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Findthe angle made by the string with the vertical.
View SolutionA body is suspended by a string from the ceiling of an elevator. It is observed that the tension in the string is doubled when the elevator is accelerated. The acceleration will be
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View Solution

