A pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
mgsinθ
mg
qEsinθ
qEcosθ
The correct Answer is:C
To find the tension in the string of a pendulum bob with mass m and charge q in a uniform horizontal electric field E, we can follow these steps:
Step 1: Analyze the Forces Acting on the Pendulum Bob
The forces acting on the pendulum bob are:
1. The gravitational force →Fg=mg acting vertically downward.
2. The tension →T in the string, which acts along the string at an angle θ with the vertical.
3. The electric force →Fe=q→E acting horizontally due to the electric field.
Step 2: Resolve the Tension into Components
The tension →T can be resolved into two components:
- The vertical component: Tcosθ
- The horizontal component: Tsinθ
Step 3: Set Up the Equations
In the vertical direction, the forces must balance:
Tcosθ=mg(1)
In the horizontal direction, the electric force must balance the horizontal component of the tension:
Tsinθ=qE(2)
Step 4: Solve for Tension
From equation (1), we can express T:
T=mgcosθ(3)
From equation (2), we can also express T:
T=qEsinθ(4)
Step 5: Equate the Two Expressions for Tension
Setting equations (3) and (4) equal to each other gives:
mgcosθ=qEsinθ
Step 6: Rearranging to Find Tension
Cross-multiplying gives:
mgsinθ=qEcosθ
Now, we can solve for T:
T=qEsinθ
Final Answer
Thus, the tension in the string is:
T=qEsinθ
The forces acting on the pendulum bob are:
1. The gravitational force →Fg=mg acting vertically downward.
2. The tension →T in the string, which acts along the string at an angle θ with the vertical.
3. The electric force →Fe=q→E acting horizontally due to the electric field.
The tension →T can be resolved into two components:
- The vertical component: Tcosθ
- The horizontal component: Tsinθ
In the vertical direction, the forces must balance:
Tcosθ=mg(1)
Tsinθ=qE(2)
From equation (1), we can express T:
T=mgcosθ(3)
T=qEsinθ(4)
Setting equations (3) and (4) equal to each other gives:
mgcosθ=qEsinθ
Cross-multiplying gives:
mgsinθ=qEcosθ
T=qEsinθ
Thus, the tension in the string is:
T=qEsinθ
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
A pendulum bob of mass 80mg and carrying a charge of 2×10−8C is at rest in a uniform, horizontal electric field of 20k Vm−1. Find the tension in the thread.
View SolutionA pendulum bob of mass 80mg and carrying a charge of 2×10−4 coulomb is at rest in a uniform horizontal electric field of 20kVm.The tension in the thread of the pendulum is x times10−4 N.Find value of x?
View Solution
Knowledge Check
A small ball of masss m and charge +q tied with a string of length l, rotating in a veticle circle under gravity and a uniform horizontal electric field E as shown. The tension in the string will be minimum for
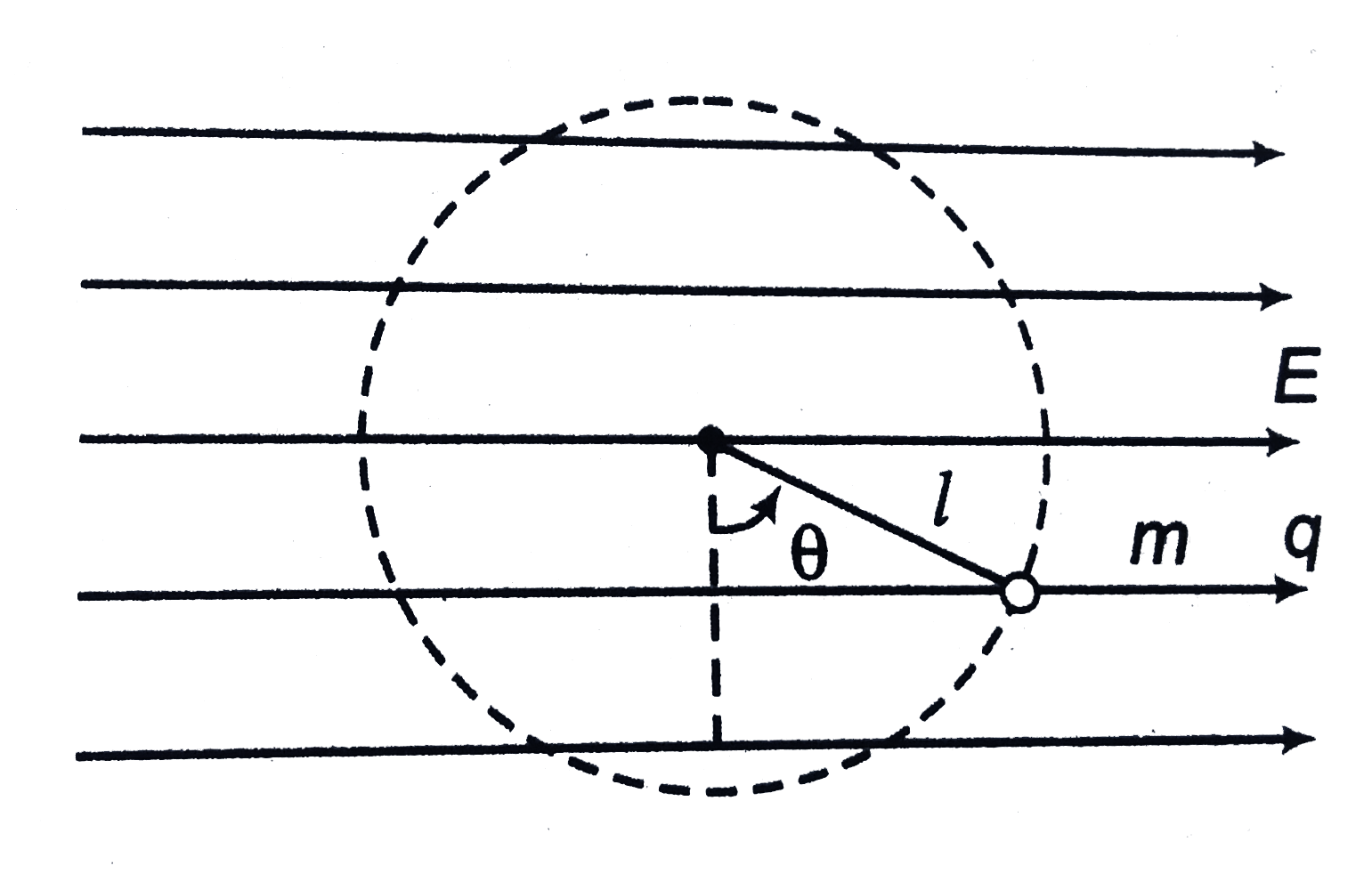 Aθ=tan−1(qEmg)Bθ=πCθ=0∘Dθ=π+tan−1(qEmg)
Aθ=tan−1(qEmg)Bθ=πCθ=0∘Dθ=π+tan−1(qEmg)A 1N pendulum bob is held at an angle θ from the vertical by a 2N horizontal force F as shown in figure. The The tension in the string supporting the pendulum bob (in newton) is
 .AcosθB2cosθC√5D1
.AcosθB2cosθC√5D1A 1N pendulum bob is held at an angle θ from the vertical by a 2 N horizontal force F as shown in the figure. The tension in the string supporting the pendulum bob (in newton) is
 AcosθB2cosθC√5D1
AcosθB2cosθC√5D1
A pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View SolutionA pendulum bob of mass m = 80 mg, carrying a charge of q=2×10−8C, is at rest in a horizontal, uniform electric field of E = 20,000 V/m. The tension T in the thread of the pendulum and the angle α it makes with vertical, is (take g=9.8m/s2)
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA body of mass mis suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionThe bob of a pendulum of length 980 cm is released from rest with its string making an angle 60∘ with the vertical. It collides with a ball of mass 20 gm resting on a smooth horizontal surface just at the position of rest of the pendulum. With what velocity will the bob move immediately after the collision? What will be the maximum angular displacement of the bob after them collision ? The mass of the bob is 10 gm. '
View Solution
