A certain charge Q is divided into two parts q and Q−q, wheich are then separated by a cetain distance. What must q be in terms of Q to maximum the electrostatic repulsion between the two charges?
The correct Answer is:B
To solve the problem of maximizing the electrostatic repulsion between two charges q and Q−q, we can follow these steps:
Step 1: Write the expression for electrostatic force
The electrostatic force F between two charges q and Q−q separated by a distance r is given by Coulomb's law:
F=kq(Q−q)r2
where k is Coulomb's constant, k=14πϵ0.
Step 2: Rewrite the force equation
Substituting k into the equation, we have:
F=14πϵ0q(Q−q)r2
Step 3: Differentiate the force with respect to q
To find the value of q that maximizes the force, we need to differentiate F with respect to q and set the derivative equal to zero:
dFdq=14πϵ0r2(Q−2q)=0
Step 4: Solve for q
Setting the derivative equal to zero gives:
Q−2q=0
Solving for q:
2q=Q⇒q=Q2
Step 5: Conclusion
Thus, to maximize the electrostatic repulsion between the two charges, the value of q must be:
q=Q2
The electrostatic force F between two charges q and Q−q separated by a distance r is given by Coulomb's law:
Substituting k into the equation, we have:
To find the value of q that maximizes the force, we need to differentiate F with respect to q and set the derivative equal to zero:
Setting the derivative equal to zero gives:
Thus, to maximize the electrostatic repulsion between the two charges, the value of q must be:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE
6 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason
19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
A certain charge Q is divided into two parts q and (Q–q). How should the charges Q and q be divided so that q and (Q–q) placed at a certain distance apart experience maximum electrostatic repulsion ?
View SolutionA charge 'Q' is divided into two parts A and B the two parts are separated by a certain fixed distance. Find for what charges on A and B would the force between them be maximum and comment when the force is minimum.
View Solution
Knowledge Check
A certain charge Q is divided at first into two parts, q and Q-q. later on the charges are placed at a certain distance. If he force of interaction between two charges is maximum, then
AQq=41BQq=21CQq=31DQq=13Charge Q is divided into two parts which are then kept some distance apart . The force between them will be maximum if the two parts are
AQ2 and Q2BQ2 and 3Q4CQ2 and 2Q3De and (Q−e)Two point charges Q and −Q/4 are separated by a distance X. Then
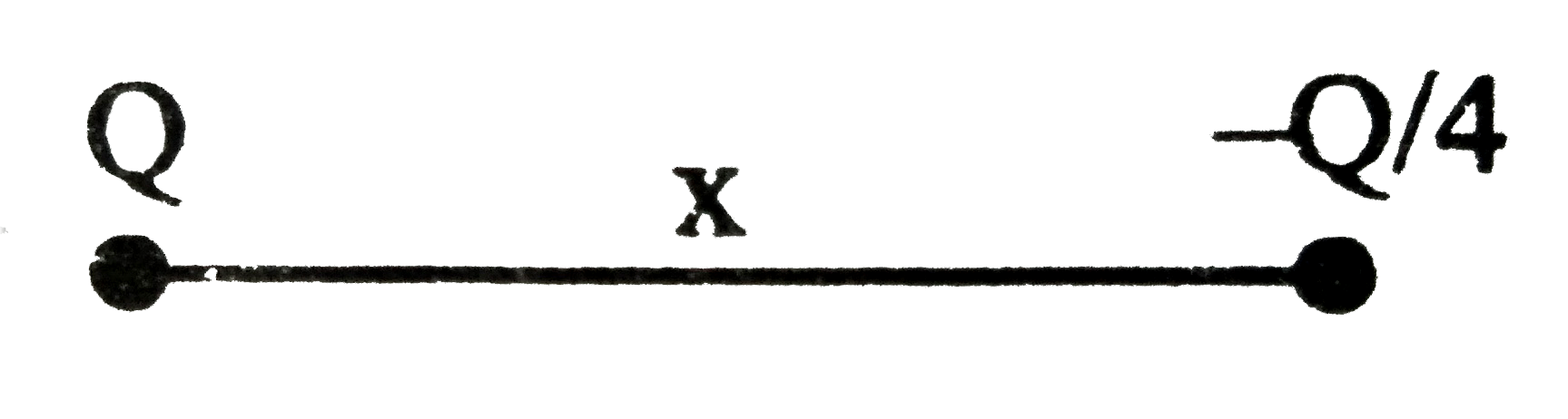 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
A charge is divided into two charges q and (Q-q) .The value of q so that force between them is maximum is equal to
View SolutionA charge Q is divided into two parts of q and Q -q . If the coulomb repulsion between them when they are separated is to be maximum, the ratio of Qq should be
View SolutionA charge Q is divided into two parts q1 and q2 such that they experience maximum force of repulsion when separated by certain distance. The ratio of Q,q1 and q2 is
View SolutionMagnitude of force between two point charges q1 and q2 which are separated by a distance r is given by
View Solutiontwo charge +q and −q are situated at a certain distance. At the point exactly midway between them
View Solution
