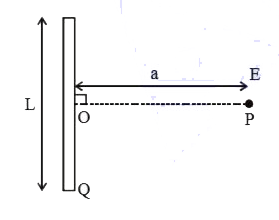
Find the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
The correct Answer is:A, B, D
To find the electric field at a point P on the perpendicular bisector of a uniformly charged rod, we can follow these steps:
Step 1: Understand the Configuration
We have a uniformly charged rod of length L with a total charge Q. The point P is located at a distance a from the center of the rod along the perpendicular bisector.
Step 2: Define the Charge Distribution
The charge per unit length λ of the rod can be defined as:
λ=QL
This means that for a small segment dx of the rod, the charge dQ can be expressed as:
dQ=λdx=QLdx
Step 3: Set Up the Electric Field Contribution
Consider a small segment dx of the rod located at a distance x from the center. The distance r from this segment to point P is given by:
r=√a2+x2
The electric field dE due to this small charge dQ at point P is given by Coulomb's law:
dE=kdQr2=kdQa2+x2
where k is Coulomb's constant.
Step 4: Resolve the Electric Field into Components
Since we are interested in the vertical component of the electric field (the component along the line connecting the rod to point P), we need to consider the angle θ that the line from the charge segment to point P makes with the horizontal. We can express the vertical component as:
dEy=dEcosθ
Using the relationship cosθ=ar, we have:
dEy=dE⋅ar=kdQa2+x2⋅a√a2+x2=kadQ(a2+x2)3/2
Step 5: Integrate Over the Length of the Rod
To find the total electric field Ey at point P, we integrate dEy from −L2 to L2:
Ey=∫L2−L2kadQ(a2+x2)3/2
Substituting dQ=QLdx:
Ey=∫L2−L2kaQLdx(a2+x2)3/2
This simplifies to:
Ey=kQaL∫L2−L2dx(a2+x2)3/2
Step 6: Evaluate the Integral
The integral can be evaluated using the substitution x=atanθ:
dx=asec2θdθ
This transforms the limits of integration and allows us to solve the integral.
Step 7: Final Expression for Electric Field
After evaluating the integral, we find the expression for the electric field Ey at point P:
Ey=2kQL⋅a√4a2+L2
Final Answer
Thus, the electric field at point P on the perpendicular bisector of the uniformly charged rod is:
E=2kQL⋅a√4a2+L2
We have a uniformly charged rod of length L with a total charge Q. The point P is located at a distance a from the center of the rod along the perpendicular bisector.
The charge per unit length λ of the rod can be defined as:
λ=QL
This means that for a small segment dx of the rod, the charge dQ can be expressed as:
dQ=λdx=QLdx
Consider a small segment dx of the rod located at a distance x from the center. The distance r from this segment to point P is given by:
r=√a2+x2
The electric field dE due to this small charge dQ at point P is given by Coulomb's law:
dE=kdQr2=kdQa2+x2
where k is Coulomb's constant.
Since we are interested in the vertical component of the electric field (the component along the line connecting the rod to point P), we need to consider the angle θ that the line from the charge segment to point P makes with the horizontal. We can express the vertical component as:
dEy=dEcosθ
Using the relationship cosθ=ar, we have:
dEy=dE⋅ar=kdQa2+x2⋅a√a2+x2=kadQ(a2+x2)3/2
To find the total electric field Ey at point P, we integrate dEy from −L2 to L2:
Ey=∫L2−L2kadQ(a2+x2)3/2
Substituting dQ=QLdx:
Ey=∫L2−L2kaQLdx(a2+x2)3/2
This simplifies to:
Ey=kQaL∫L2−L2dx(a2+x2)3/2
The integral can be evaluated using the substitution x=atanθ:
dx=asec2θdθ
This transforms the limits of integration and allows us to solve the integral.
After evaluating the integral, we find the expression for the electric field Ey at point P:
Ey=2kQL⋅a√4a2+L2
Thus, the electric field at point P on the perpendicular bisector of the uniformly charged rod is:
E=2kQL⋅a√4a2+L2
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Level 1 Subjective
Explore 15 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:SUBJECTIVE_TYPE
Explore 6 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Level 1 Assertion And Reason
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
Similar Questions
The electric foield at a point A on the perpendicular bisector of a uniformly charged wire of length l=3m and total charge q = 5 nC is x V/m. The distance of A from the centre of the wire is b = 2m. Find the value of x.
View SolutionFind : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.
View Solution
Knowledge Check
Find the electric field at point P (as shown in figure) on the perpendicular bisector of a uniformly charged thin wire of length L carrying a charge Q. The distance of the point P from the centre of the rod is a =√32L.
 A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2A point P lies on the perpendicular bisector of a short electric dipole, of dipole moment p' at a distance r from the centre of dipole. The electric field at point P is proportional to
APr2B1pr2Cpr3Dp2r3
Calculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =λ) of length 2l at a distance a from the centre of the rod.
View SolutionThe electric field at a point P which is at a distance l on the perpendicular bisector of a uniformly charged wire of length 1 , charge Q=(Q)/(2 pi varepsilon_(0)l^(2)sqrt(k)) where k = ?
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View SolutionA charge of 1 coul. is placed at one end of a non-conducting rod of length 0.6m. the rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency 104πradian/sec. Find the magnetic field at a point on the axis ofrotation at a distance of 0.8 from the centre of the path. Now half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about horizontal axis passing through the mid-point of the rod with the same angnlar frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4m form the centre of the rod.
View SolutionCalculate electric field intensity at point P due to a thin positive uniformly charged rod . Point P is at perpendicular distance d from the rod . The lower and upper ends of the rod make the angles α and β as shown below .
View Solution

