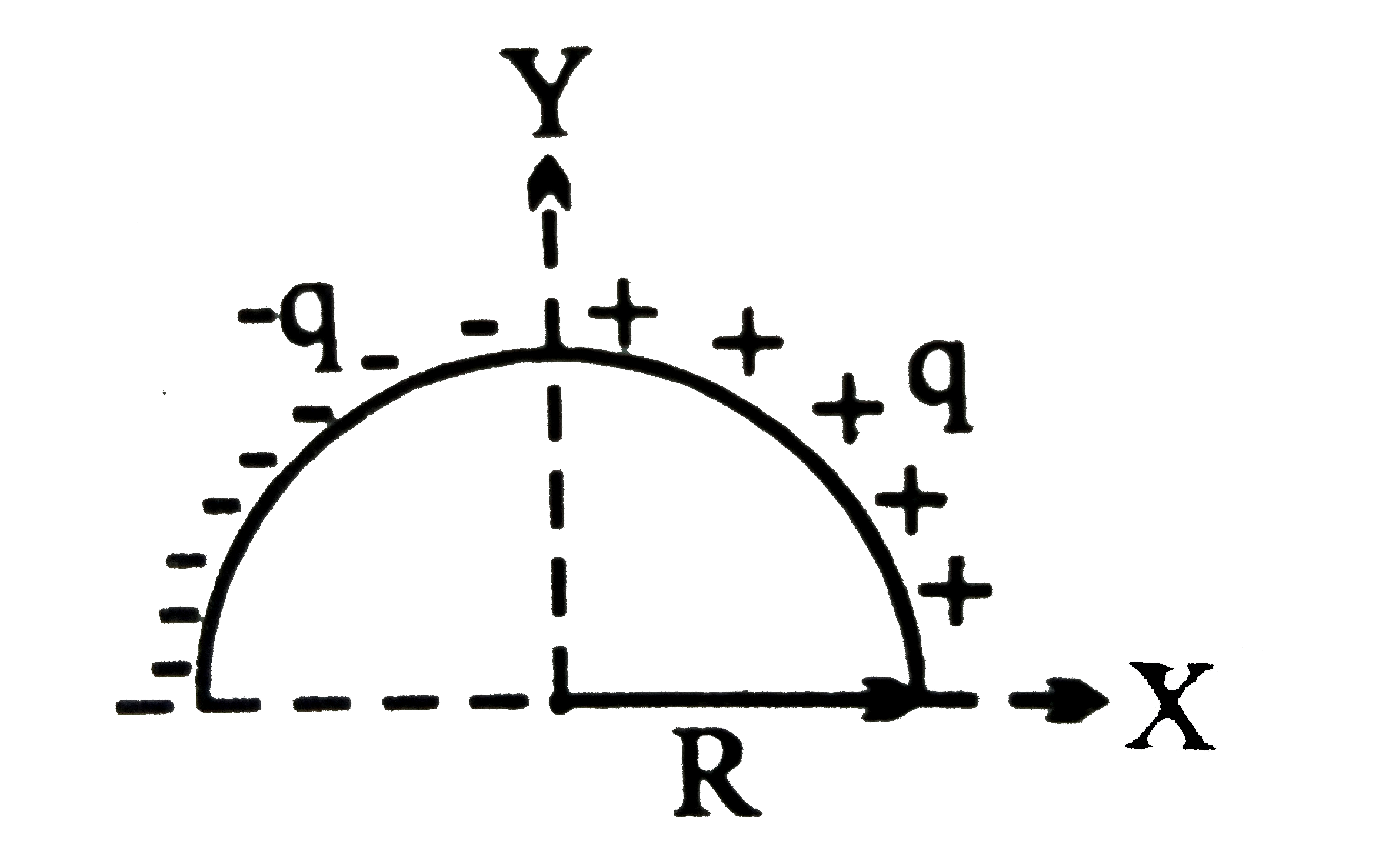
Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
The correct Answer is:A, B, D
To find the electric field at the center of a uniformly charged semicircular ring of radius R with a linear charge density λ, we can follow these steps:
Step 1: Define the Charge Element
Consider a small charge element dq on the semicircular ring. The linear charge density λ is defined as the charge per unit length. Thus, for a small arc length dθ at radius R:
dq=λ⋅dL=λ⋅R⋅dθ
Step 2: Set Up the Electric Field Contribution
The electric field dE due to the charge element dq at the center of the semicircular ring can be expressed using Coulomb's law:
dE=k⋅dqR2
Where k is Coulomb's constant, k=14πϵ0.
Substituting for dq:
dE=k⋅λ⋅R⋅dθR2=k⋅λR⋅dθ
Step 3: Resolve the Electric Field Components
The electric field dE has both horizontal (x-direction) and vertical (y-direction) components. Due to symmetry, the horizontal components from opposite sides will cancel out, and we only need to consider the vertical components.
The vertical component dEy is given by:
dEy=dE⋅sinθ
Where θ is the angle corresponding to the position of the charge element on the semicircle.
Step 4: Substitute for dE
Substituting for dE:
dEy=k⋅λR⋅dθ⋅sinθ
Step 5: Integrate Over the Semicircle
To find the total electric field Ey at the center, integrate dEy from θ=0 to θ=π:
Ey=∫π0dEy=∫π0k⋅λR⋅sinθdθ
Step 6: Evaluate the Integral
The integral of sinθ is:
∫sinθdθ=−cosθ
Thus, evaluating the definite integral:
Ey=k⋅λR(−cosθ)π0=k⋅λR(−(−1)−(−1))=k⋅λR⋅2
Step 7: Final Expression for Electric Field
Substituting k=14πϵ0:
Ey=2k⋅λR=2⋅14πϵ0⋅λR=λ2πϵ0R
Conclusion
The electric field at the center of the uniformly charged semicircular ring is:
E=λ2πϵ0R
Consider a small charge element dq on the semicircular ring. The linear charge density λ is defined as the charge per unit length. Thus, for a small arc length dθ at radius R:
The electric field dE due to the charge element dq at the center of the semicircular ring can be expressed using Coulomb's law:
The electric field dE has both horizontal (x-direction) and vertical (y-direction) components. Due to symmetry, the horizontal components from opposite sides will cancel out, and we only need to consider the vertical components.
Substituting for dE:
To find the total electric field Ey at the center, integrate dEy from θ=0 to θ=π:
The integral of sinθ is:
Substituting k=14πϵ0:
The electric field at the center of the uniformly charged semicircular ring is:
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Level 1 Subjective
Explore 15 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:SUBJECTIVE_TYPE
Explore 6 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Level 1 Assertion And Reason
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:All Questions
Explore 120 Videos
Similar Questions
Knowledge Check
Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
Ar−1BrCr2Dr−2The electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπR
In the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
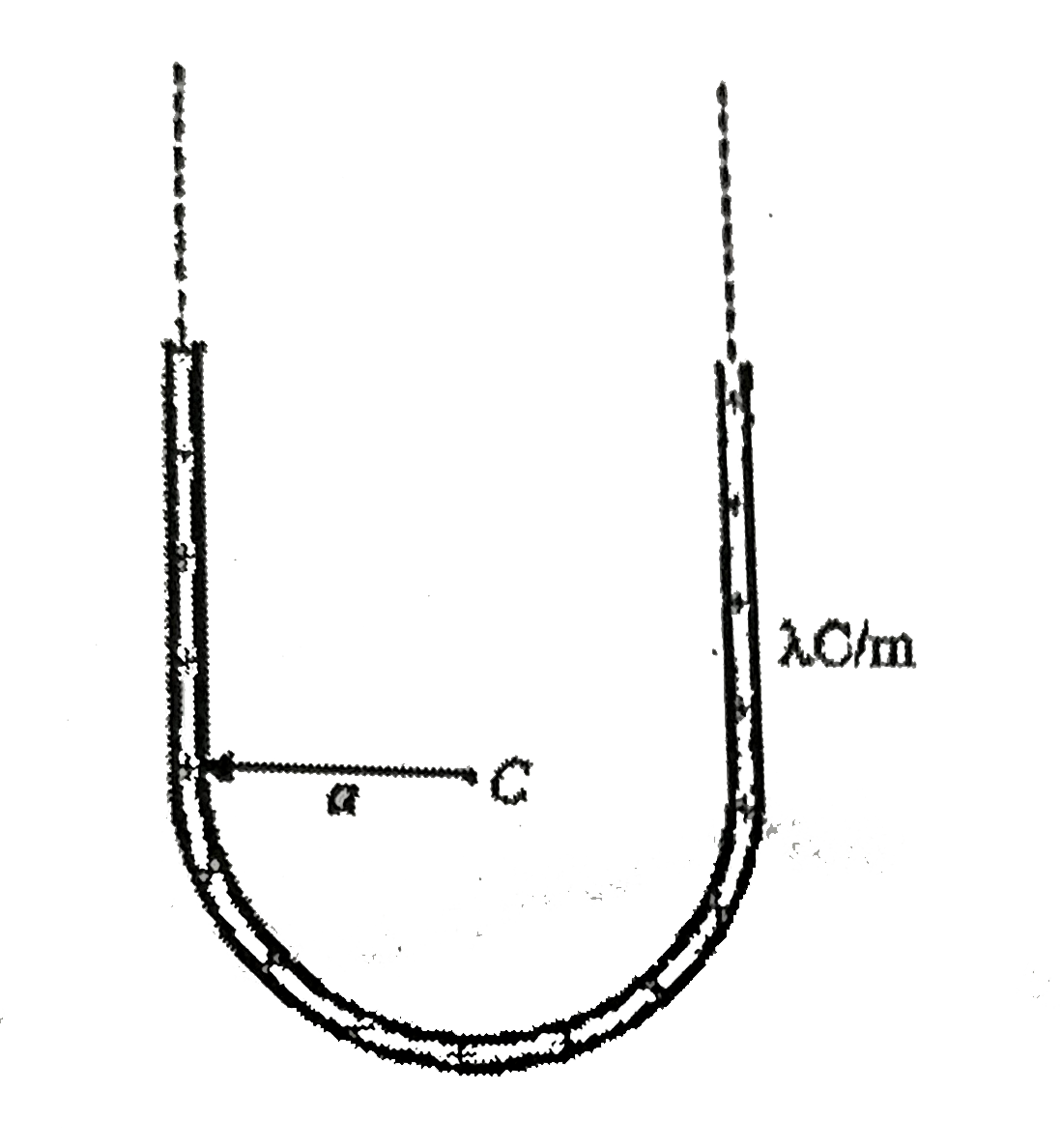
View SolutionElectric field at centre O of semicircule of radius 'a' having linear charge density λ given is given by

View SolutionElectric field at the centre of uniformly charge hemispherical shell of surface charge density σ is σnε0 then find the value of n.

View SolutionIf coulomb's law were F=KqQr3, calculate the electric field due to a uniformly charged line charge at a distance d from it. The linear charge density on the line charge is λ C/m, and it is of infinite length.
View SolutionDraw the electric field vs distance (from the centre ) graph for (i) a long charged rod having linear charge density λ>0 (ii) spherical shell of radius R and charge Q>0 .
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View Solution


 .
.