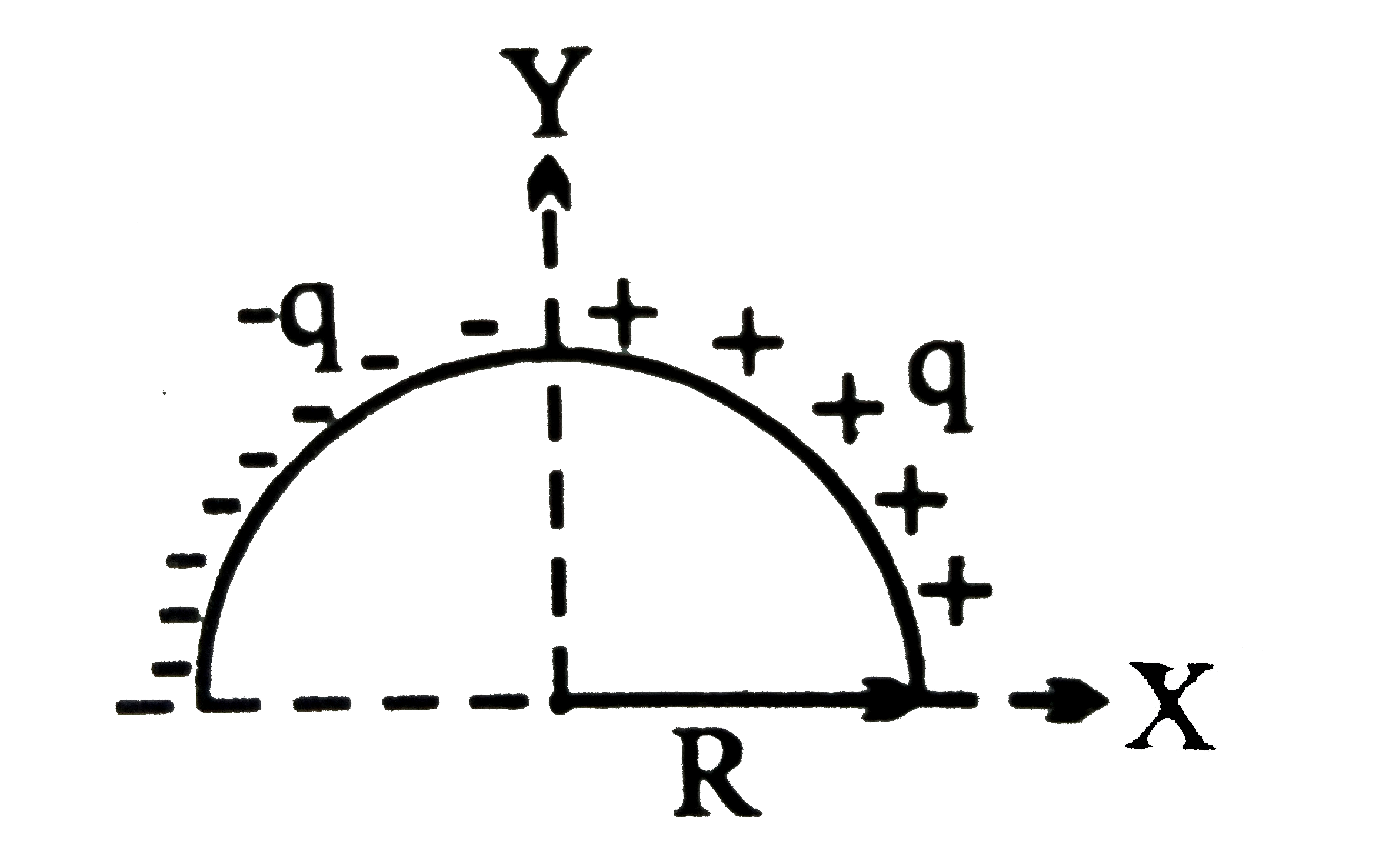
Find the electric field at the centre of a semicircular ring if it is uniformly positive charged.
To find the electric field at the center of a uniformly positively charged semicircular ring, we can follow these steps:
1. Define the Problem:
- We have a semicircular ring of radius R with a uniform linear charge density λ. We need to find the electric field at the center of the semicircle.
2. Consider a Small Element:
- Take a small element ds of the semicircular ring. The charge dq on this element can be expressed as:
dq=λds
- The length of the small element ds can be related to the angle dθ as:
ds=Rdθ
- Thus, we can rewrite dq:
dq=λRdθ
3. Calculate the Electric Field Contribution:
- The electric field dE at the center due to the charge dq is given by Coulomb's law:
dE=14πϵ0dqR2=14πϵ0λRdθR2=λ4πϵ0Rdθ
4. Resolve the Electric Field into Components:
- The electric field dE makes an angle θ with the vertical. Thus, we can resolve dE into vertical and horizontal components:
- The vertical component dEy:
dEy=dEcosθ=λ4πϵ0Rdθcosθ
- The horizontal component dEx:
dEx=dEsinθ=λ4πϵ0Rdθsinθ
5. Integrate Over the Semicircle:
- The horizontal components dEx from opposite sides of the semicircle will cancel out due to symmetry. Therefore, we only need to integrate the vertical components dEy:
Ey=∫π2−π2dEy=∫π2−π2λ4πϵ0Rcosθdθ
6. Evaluate the Integral:
- The integral of cosθ from −π2 to π2 is:
∫π2−π2cosθdθ=(sinθ)π2−π2=sin(π2)−sin(−π2)=1−(−1)=2
- Thus, we have:
Ey=λ4πϵ0R⋅2=λ2πϵ0R
7. Final Result:
- The electric field at the center of the semicircular ring is directed vertically upwards and has a magnitude of:
E=λ2πϵ0R
- We have a semicircular ring of radius R with a uniform linear charge density λ. We need to find the electric field at the center of the semicircle.
- Take a small element ds of the semicircular ring. The charge dq on this element can be expressed as:
dq=λds
- The length of the small element ds can be related to the angle dθ as:
ds=Rdθ
- Thus, we can rewrite dq:
dq=λRdθ
- The electric field dE at the center due to the charge dq is given by Coulomb's law:
dE=14πϵ0dqR2=14πϵ0λRdθR2=λ4πϵ0Rdθ
- The electric field dE makes an angle θ with the vertical. Thus, we can resolve dE into vertical and horizontal components:
- The vertical component dEy:
dEy=dEcosθ=λ4πϵ0Rdθcosθ
- The horizontal component dEx:
dEx=dEsinθ=λ4πϵ0Rdθsinθ
- The horizontal components dEx from opposite sides of the semicircle will cancel out due to symmetry. Therefore, we only need to integrate the vertical components dEy:
Ey=∫π2−π2dEy=∫π2−π2λ4πϵ0Rcosθdθ
- The integral of cosθ from −π2 to π2 is:
∫π2−π2cosθdθ=(sinθ)π2−π2=sin(π2)−sin(−π2)=1−(−1)=2
- Thus, we have:
Ey=λ4πϵ0R⋅2=λ2πϵ0R
- The electric field at the center of the semicircular ring is directed vertically upwards and has a magnitude of:
E=λ2πϵ0R
Topper's Solved these Questions
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 10 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 15 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBook:FIITJEEChapter:ELECTROMAGNETIC WAVE & WAVE OPTICSExercise:ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
Explore 21 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
Similar Questions
Knowledge Check
The electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπRThe moment of inertia of semicircular ring about its centre is
AMR2BMR22CMR24DNone of theseA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32
Find the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA ring of radius R has uniformly distributed charge q. A point charge Q is placed at the centre of the ring. (a) Find the increase in tension in the ring after the point charge is placed at its centre. (b) Find the increase in force between the two semicircular parts of the ring after the point charge is placed at the centre. (c) Using the result found in part (b) find the force that the point charge exerts on one half of the ring.
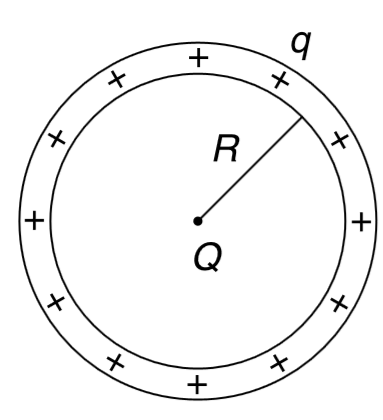
View SolutionA circular ring lying in the x-y plane with its centre at the origin carries a uniformly distributed positive charge. The variation of the electric field E at the point (0,0,z) is correctly represented by the graph is
View SolutionA thin conducting ring orf radius R is given a chareg +Q, Fig. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on part ACDB of the ring is

View Solution


 .
.