An infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the center of the hole.

Potential function is not defined for infinite conducting sheet and hence to solve this either calculate potential difference or use force equations
Electric field due to infinite dielectric sheet, E1=σ2ε0
Electric field at the axis of a disc of radius R.
E2=σ2ε0[1−x√x2−R2]
Resultant electric field E=E1−E2=σ2ε0−x√x2+R2
Force on the direction
F=−σex2ε0√x2+R2
mvdvdx=−σex2ε0√x2+R2
m∫v0vdv=−σe2ε0∫0√3R=x√x2+R2dx
mv22=−σe2ε0[√x2+R2]0√3R
v=√σeRmε0
Topper's Solved these Questions
Similar Questions
An infinite dielectric sheet having charge density σ has a holeof radius R in it. An electrom is released from point P on the axis of the hole at a distance √3R from the center. Find the speed with which it crosses the plane of the sheet.
 .
.
View SolutionA uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View Solution
Knowledge Check
There is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
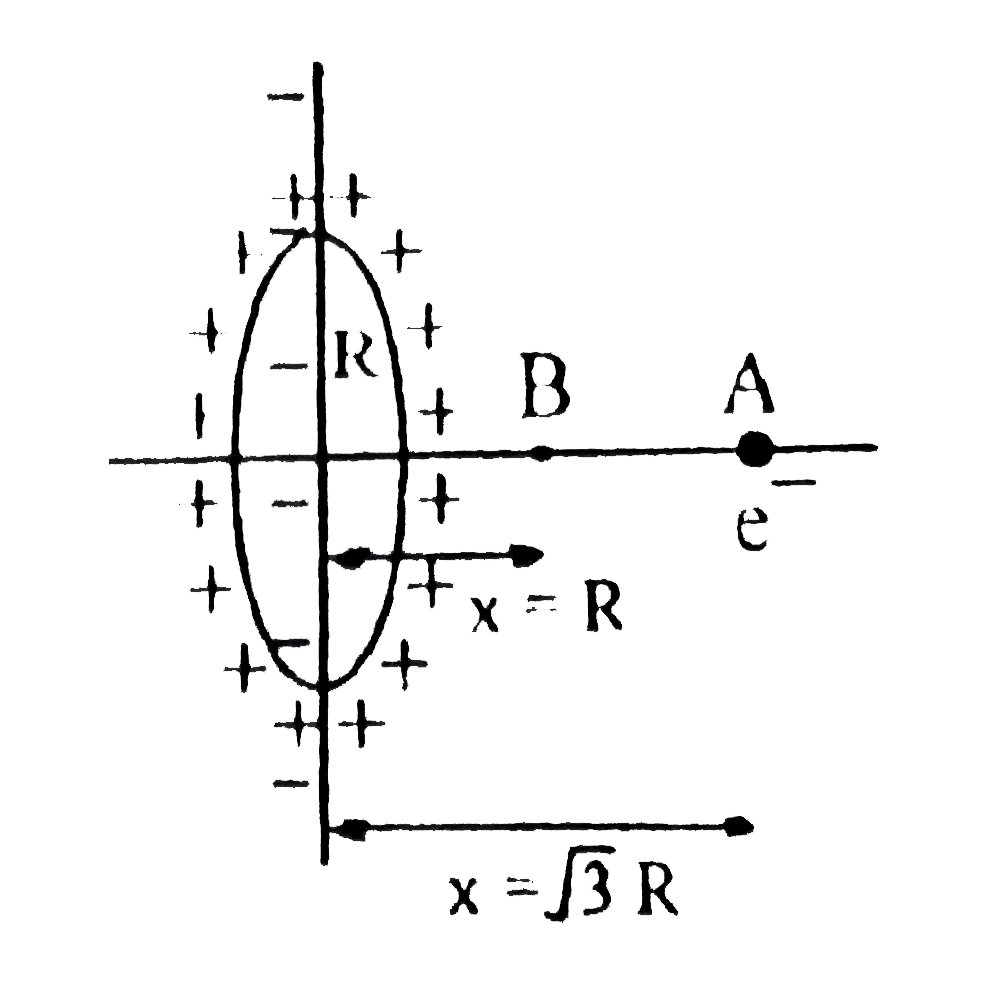
The distance from centre of ring on the axis where the net force on the electron is zero.A2RB√2RCRDnone of theseThere is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
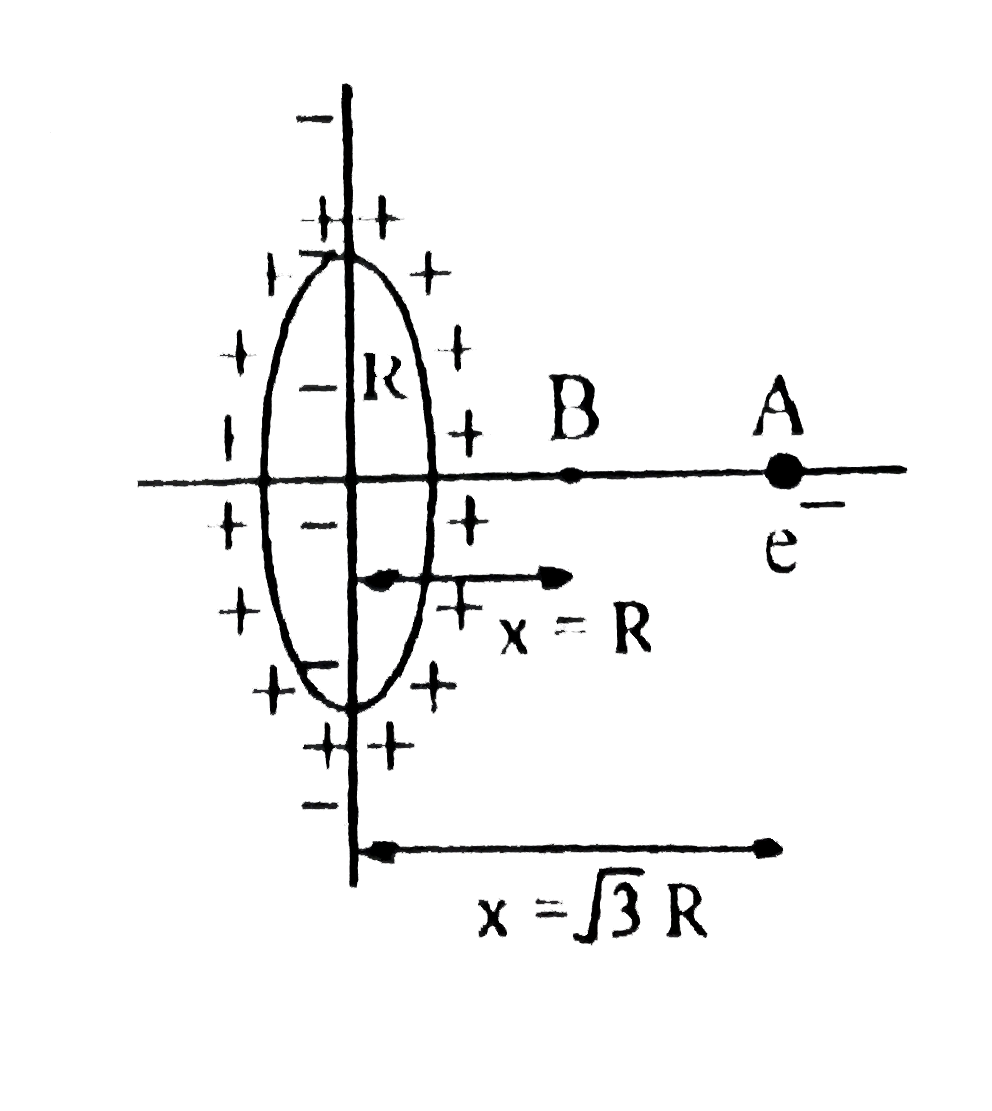
Magnitude of initial acceleration of the electron.Aeλπɛ0mR(3−2√24√6)Beλπɛ0mR(3+2√24√6)Ceλπɛ0mR(3+2√24√3)DnoneA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
A14πε0q2RB14πε04q3RC14πε05q6RD14πε02q3R
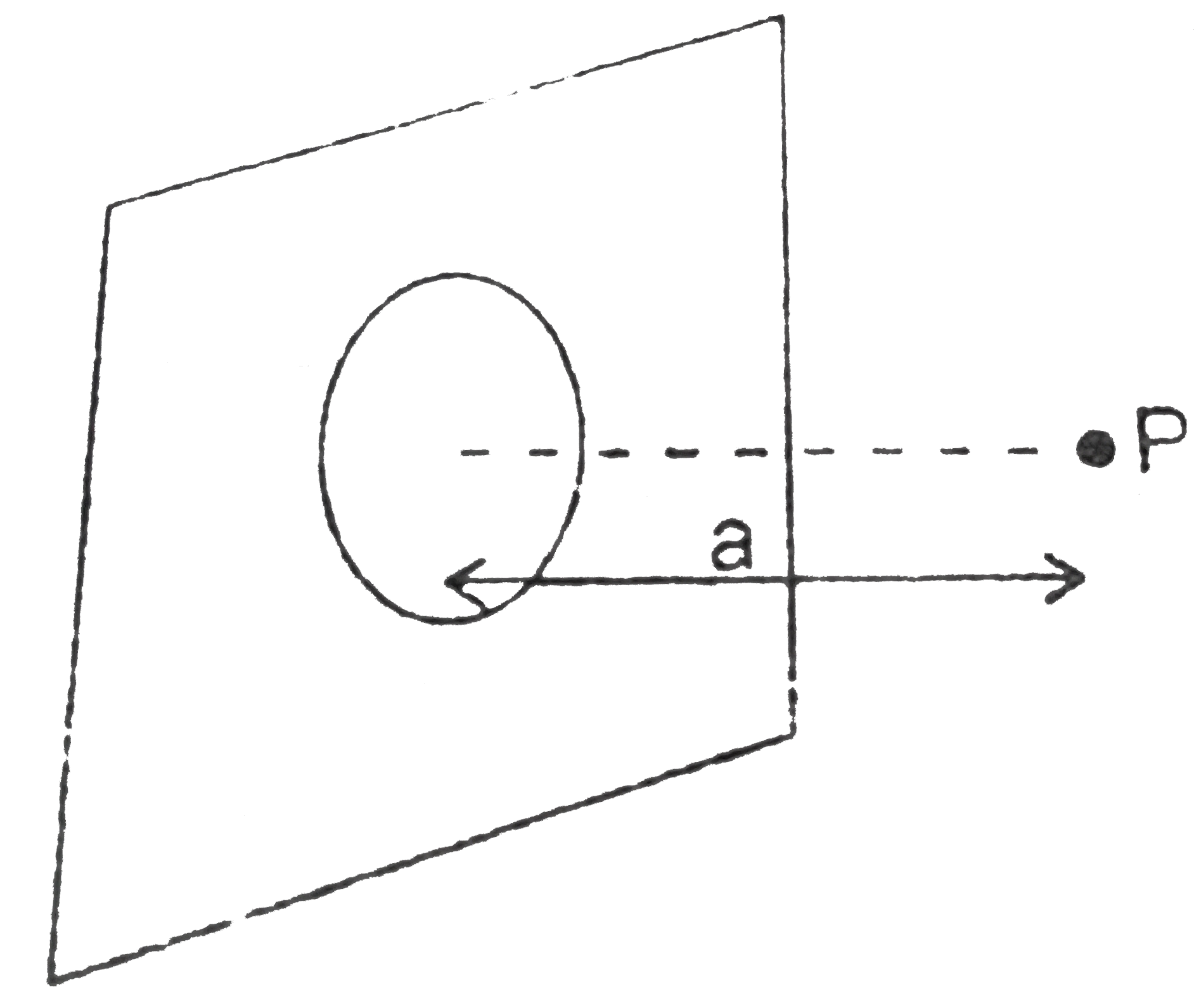
An infinitely large non-conducting plane of uniform surface charge density σ has circular aperture of certain radius carved out from it. The electric field at a point which is at a distance 'a' from the centre of the aperture (perpendicular to the plane) is σ2√2∈0. Find the radius of aperture :
View SolutionA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
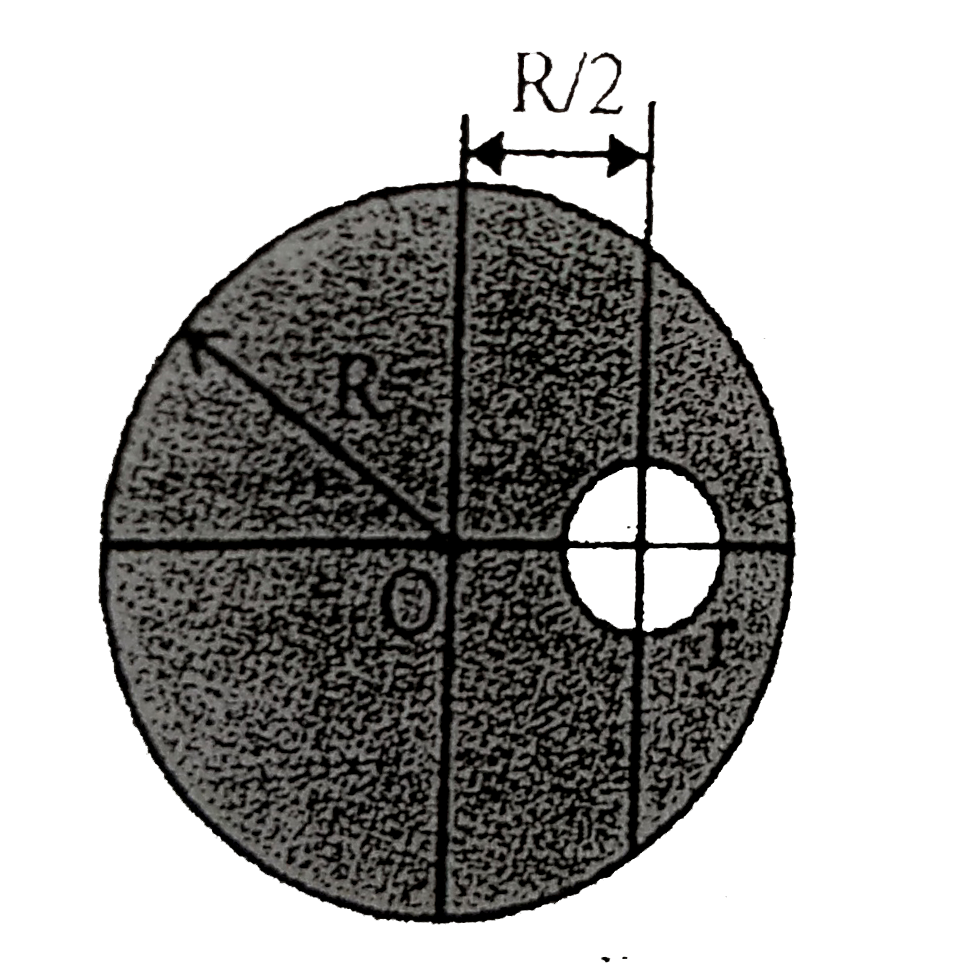
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
View SolutionThere is a uniformly charged ring having radius R. An infinite line charge (charge per unit length lambda) is placed along a diameter of the ring (in gravity free space). Total charge on the ring Q=4√2λR. An electron of mass m is released from rest on the axis of the ring at a distance x=√3R from the centre.
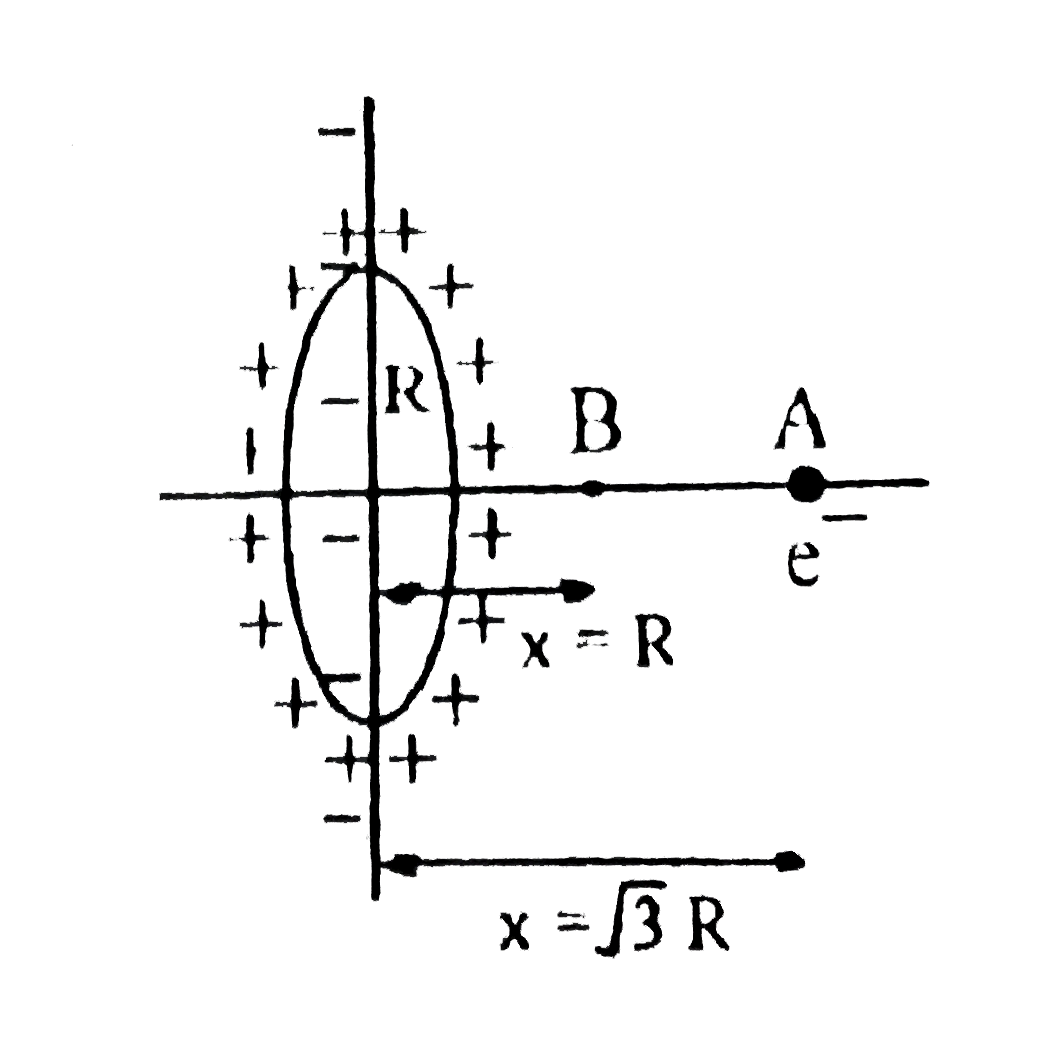
Potential difference between points A(x=√3R) and B(x=R)i.e.(VA−VB) is
View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by

View Solution

