What is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
To find the electric field intensity at any point on the axis of a charged rod of length L and linear charge density λ, where the point is separated from the nearer end by a distance A, we can follow these steps:
1. Define the Problem:
We have a uniformly charged rod of length L with a linear charge density λ. We need to find the electric field intensity at a point P located at a distance A from the nearer end of the rod.
2. Set Up the Coordinate System:
Place the rod along the x-axis. Let the left end of the rod be at the origin (0,0) and the right end at (L,0). The point P is located at (A,0).
3. Consider an Element of Charge:
Take a small element of the rod of length dx located at a distance x from the point P. The charge dq on this element is given by:
dq=λdx
4. Calculate the Electric Field Due to the Element:
The electric field dE at point P due to the charge dq is directed away from the charge (if the charge is positive) and is given by Coulomb's law:
dE=kdqr2
where r is the distance from the charge element to point P. The distance r can be expressed as:
r=|A−x|
Thus,
dE=kλdx(A−x)2
5. Integrate to Find Total Electric Field:
The total electric field E at point P is obtained by integrating dE from x=0 to x=L:
E=∫L0dE=∫L0kλdx(A−x)2
6. Perform the Integration:
The integral can be computed as follows:
E=kλ∫L0dx(A−x)2
The integral ∫dx(A−x)2 evaluates to:
−1A−x
Therefore,
E=kλ(−1A−x)L0=kλ(−1A−L+1A)
7. Simplify the Result:
This gives:
E=kλ(1A−1A−L)
To combine these fractions:
E=kλ((A−L)−AA(A−L))=kλ(−LA(A−L))
Thus, the electric field intensity at point P is:
E=kλLA(A+L)
Final Result:
The electric field intensity at point P is:
E=kλLA(A+L)
where k=14πϵ0.
We have a uniformly charged rod of length L with a linear charge density λ. We need to find the electric field intensity at a point P located at a distance A from the nearer end of the rod.
Place the rod along the x-axis. Let the left end of the rod be at the origin (0,0) and the right end at (L,0). The point P is located at (A,0).
Take a small element of the rod of length dx located at a distance x from the point P. The charge dq on this element is given by:
dq=λdx
The electric field dE at point P due to the charge dq is directed away from the charge (if the charge is positive) and is given by Coulomb's law:
dE=kdqr2
where r is the distance from the charge element to point P. The distance r can be expressed as:
r=|A−x|
Thus,
dE=kλdx(A−x)2
The total electric field E at point P is obtained by integrating dE from x=0 to x=L:
E=∫L0dE=∫L0kλdx(A−x)2
The integral can be computed as follows:
E=kλ∫L0dx(A−x)2
The integral ∫dx(A−x)2 evaluates to:
−1A−x
Therefore,
E=kλ(−1A−x)L0=kλ(−1A−L+1A)
This gives:
E=kλ(1A−1A−L)
To combine these fractions:
E=kλ((A−L)−AA(A−L))=kλ(−LA(A−L))
Thus, the electric field intensity at point P is:
E=kλLA(A+L)
The electric field intensity at point P is:
E=kλLA(A+L)
where k=14πϵ0.
Topper's Solved these Questions
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - I
Explore 14 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS
Explore 4 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 15 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBook:FIITJEEChapter:ELECTROMAGNETIC WAVE & WAVE OPTICSExercise:ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
Explore 21 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
Similar Questions
Knowledge Check
Electric field intensity at a point a hollow charged spherical conductor
Ais zeroBis constantCincrease with the distance from the centre of the sphereDnone of theseThe electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
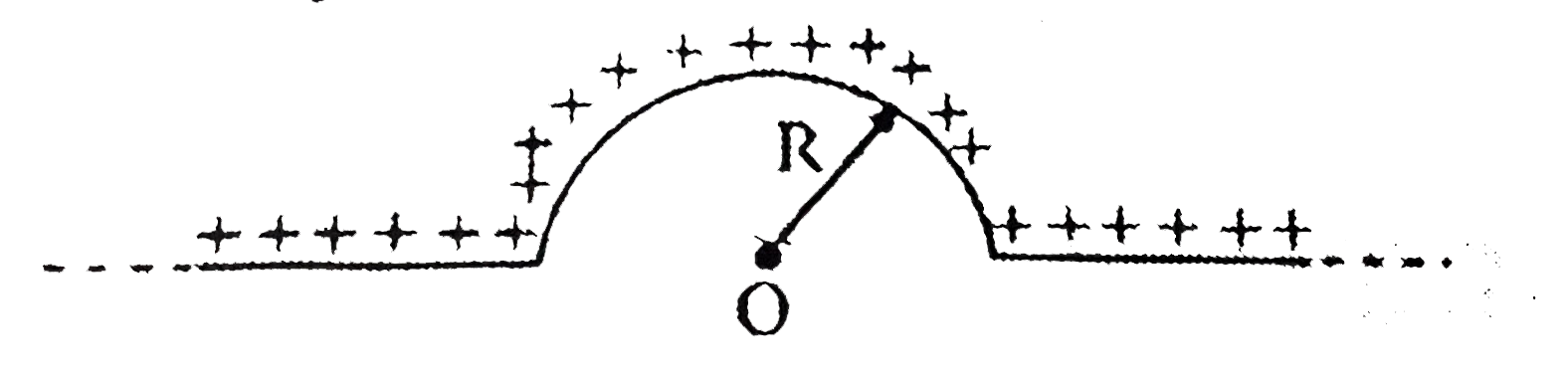 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzeroElectric intensity at a point just outside a charged conductor of any shape is
Aσ∈0KBσ2∈0KC2σ∈KDσ22∈K
Derive an expression for electric field intensity at a point due to point charge.
View SolutionWhat is electric field intensity at a point at a distance r meter from q coulomb of a charge in free space ?
View SolutionElectric field intensity at point P due to charge distributed over a sphere is:

View SolutionThe electric intensity at a point near a charged conductor of surface charge density σ is
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View Solution