A spherical Gaussian surface surrounds a point charge q. If the charge is moved to another location inside the surface? Then total flux_____________
To solve the problem, we will use Gauss's Law, which states that the electric flux (Φ) through a closed surface is directly proportional to the charge enclosed within that surface. The mathematical expression of Gauss's Law is given by:
Φ=Qencε0
where:
- Φ is the electric flux,
- Qenc is the total charge enclosed within the Gaussian surface,
- ε0 is the permittivity of free space (a constant).
1. Identify the Initial Situation:
- We have a spherical Gaussian surface that surrounds a point charge q.
- The charge q is enclosed within this surface.
2. Calculate the Initial Electric Flux:
- According to Gauss's Law, the initial electric flux (Φ1) through the surface is given by:
Φ1=qε0
3. Move the Charge Inside the Surface:
- The problem states that the charge q is moved to another location inside the same spherical Gaussian surface.
- It is important to note that even though the position of the charge has changed, it is still enclosed by the Gaussian surface.
4. Calculate the New Electric Flux:
- After moving the charge, the total charge enclosed (Qenc) remains the same, which is still q.
- Therefore, the new electric flux (Φ2) through the surface is:
Φ2=qε0
5. Compare the Initial and New Flux:
- Since Φ1=Φ2, we can conclude that the total electric flux through the spherical Gaussian surface does not change when the charge is moved to a different location inside the surface.
Conclusion:
The total flux through the spherical Gaussian surface remains unchanged when the charge is moved to another location inside the surface.
Final Answer:
The total flux remains unchanged.
---
- Φ is the electric flux,
- Qenc is the total charge enclosed within the Gaussian surface,
- ε0 is the permittivity of free space (a constant).
- We have a spherical Gaussian surface that surrounds a point charge q.
- The charge q is enclosed within this surface.
- According to Gauss's Law, the initial electric flux (Φ1) through the surface is given by:
Φ1=qε0
- The problem states that the charge q is moved to another location inside the same spherical Gaussian surface.
- It is important to note that even though the position of the charge has changed, it is still enclosed by the Gaussian surface.
- After moving the charge, the total charge enclosed (Qenc) remains the same, which is still q.
- Therefore, the new electric flux (Φ2) through the surface is:
Φ2=qε0
- Since Φ1=Φ2, we can conclude that the total electric flux through the spherical Gaussian surface does not change when the charge is moved to a different location inside the surface.
The total flux through the spherical Gaussian surface remains unchanged when the charge is moved to another location inside the surface.
The total flux remains unchanged.
Topper's Solved these Questions
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - II & III
Explore 15 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL - I
Explore 24 Videos
- ELECTROSTANTICSBook:FIITJEEChapter:ELECTROSTANTICSExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - I
Explore 14 Videos
- ELECTROMAGNETIC WAVE & WAVE OPTICSBook:FIITJEEChapter:ELECTROMAGNETIC WAVE & WAVE OPTICSExercise:ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)
Explore 21 Videos
- ELECTROSTATICSBook:FIITJEEChapter:ELECTROSTATICSExercise:Example
Explore 14 Videos
Similar Questions
Can charge lie on a Gaussian surface?
View SolutionA point charges causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charges.
If the radius of the Gaussian surface were doubled , how much flux would pass through the surface?
What is the value of the point charges?
View Solution
Knowledge Check
A Gaussian surface enclosed no charge. Which of the following is true for a point inside it ?
Aelectric field must be zeroBelectric potential must be zeroCboth electric potential and intensity must be zeroDnone of theseA point charge causes an electric flux of −200Nm2/C to pass through spherical Guassian surface of 10 cm radius centered on the charge. If the radius of the Guassian surface is doubled, the total electric flux passing through the surface is
A−200Nm2/CB−100Nm2/CC+200Nm2/CD−50Nm2/CConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
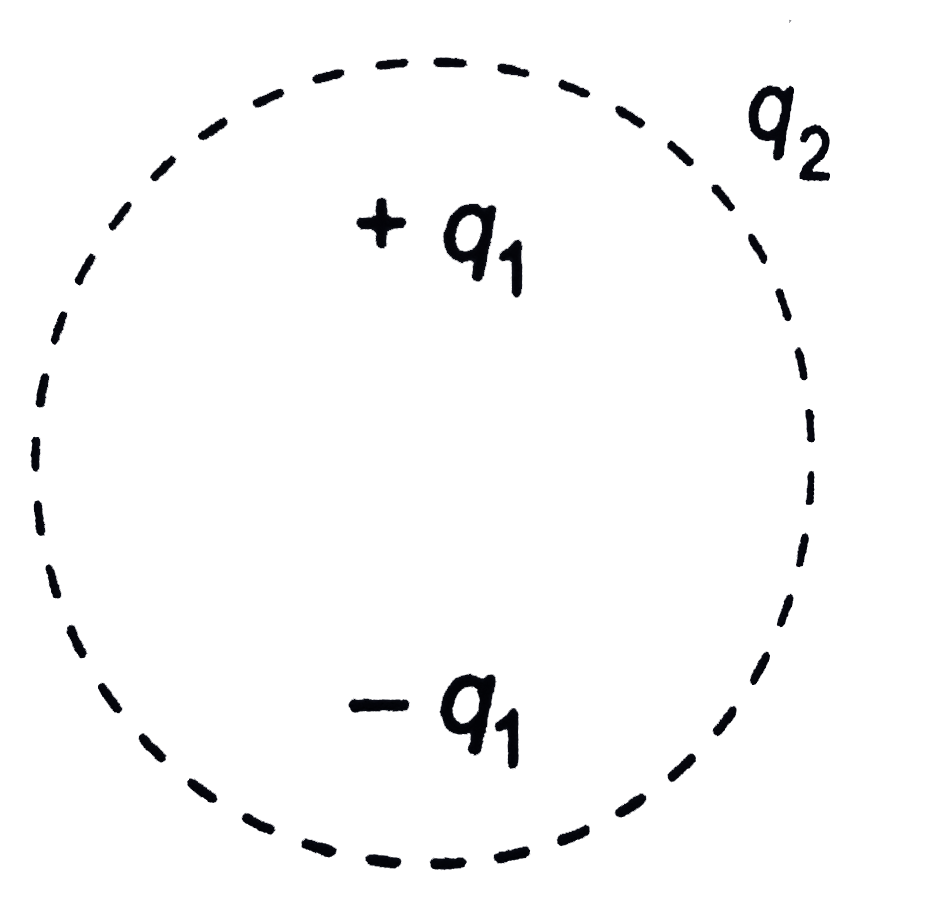 Aq2Bonly the positive chargesCall the chargesD+q1 and −q1
Aq2Bonly the positive chargesCall the chargesD+q1 and −q1
A point charge causes an electric flux of −1.0×103Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface ? (b) What is the is the value of the point charge ?
View SolutionIf net flux through a Gaussian surface is zero, then find whether the following statements are correct or not.
The net charge inside the surface is zero.
View SolutionConsider a Gaussian spherical surface covering a dipole of charge q and -q, then

View SolutionFind the total flux due to charge q associated with the given hemispherical surface
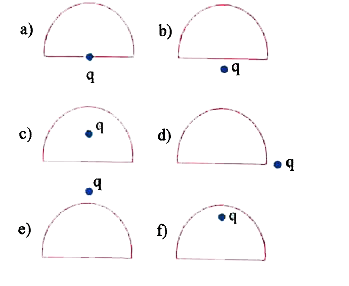
View SolutionFind the total flux due to charge qassociated with the given hemisphercal surface
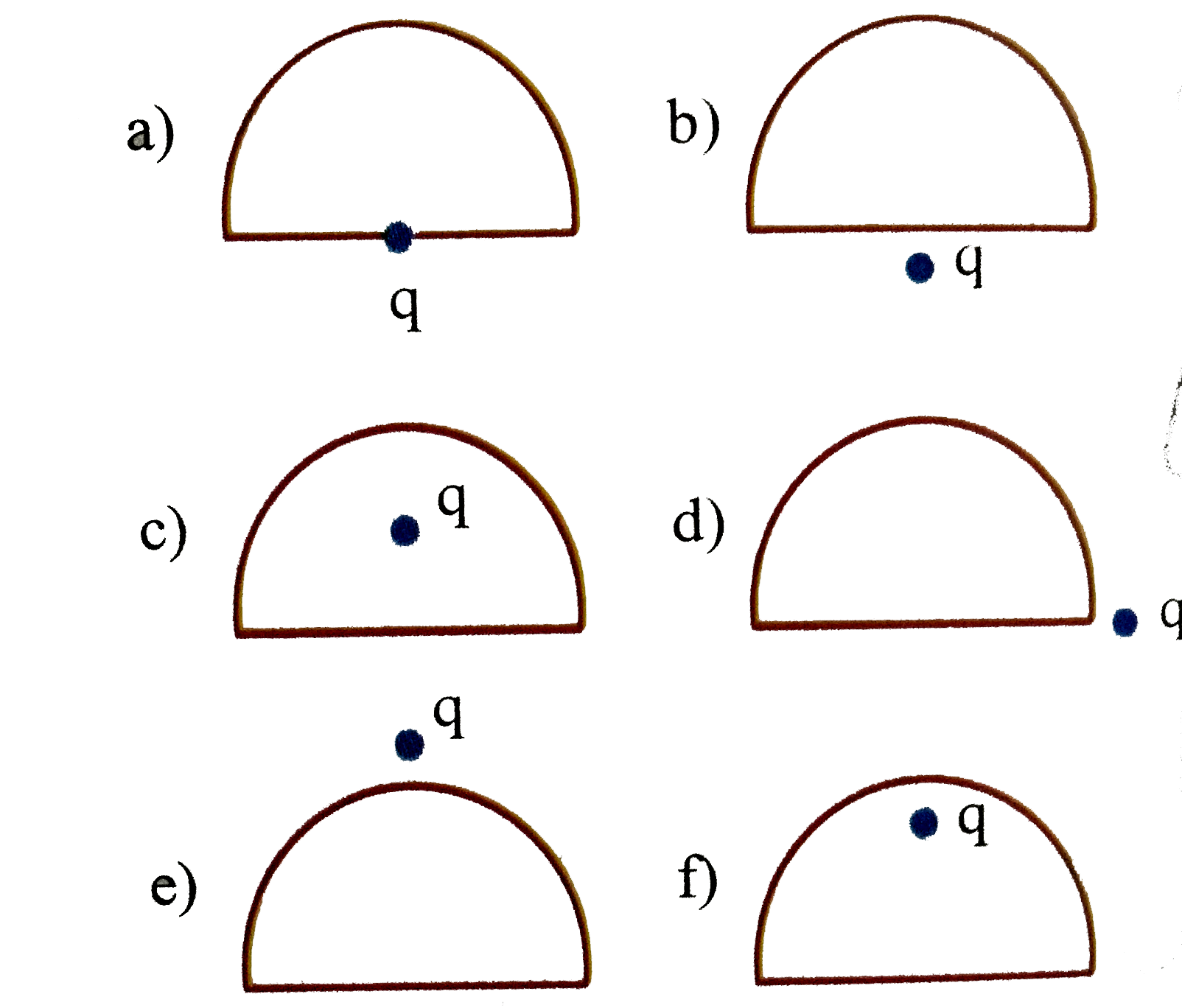
View Solution

